|
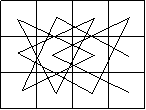
Алгоритм пошуку з поверненням. Алгоритм, що розглянуто минулого разу, ще називають пошуком в глибину. Взагалі, це не просто алгоритм, а стратегія. Чому саме так, а також чому ця стратегія має саме таку назву, які ще існують стратегії, спробуємо з'ясувати, розв'язати таку задачу. Шахівниця має розмір m*n. Шаховий кінь ходить за звичайними правилами (на 2 клітинки у деякому напрямку і на 1 у перпендикулярному). Знайти шлях коня, щоб усі клітинки шахівниці кінь побував рівно один раз. На шахівниці 3*4 шлях коня існує, а на шахівницях 3*3, 2*5 та інших не існує. Якщо на шахівниці можливі різні шляхи коня, необхідно знайти хоча б один. На малюнку показаний один з можливих шляхів коня для шахівниці 3*4.
Клітинку шахівниці зручно задавати парою чисел: номер рядка та номер стовпчика. Якщо нумерацію рядків здійснити зверху вниз, а стовпчиків – зліва направо, зображений шлях коня запишеться так: (3;4) – (2;2) – (1;4) – (3;3) – (2;1) – (1;3) – (3;2) – (1;1) – (2;3) – (3;1) – (1;2) – (2;4). Звичайно, існують інші шляхи коня на цій шахівниці. Покажемо, як можна звести розв’язання цієї задачі до пошуку шляху в деякому простому графі. Нехай клітинка – це вершина графа, а дві вершини такого графа суміжні тоді і тільки тоді, коли кінь може за один хід перейти з однієї клітинки на іншу. Знаходимо шлях довжиною, меншою на 1 за кількість клітинок.
Побудуйте матрицю суміжності графа для шахівниці, номери кліток якої наведено вище, і знайдіть шлях у такому графі, що має довжину 11 і починається у клітинці 1. Вказівка. Необхідно модифікувати алгоритм, щоб не дозволялося записувати до стеку клітинку, якщо кінь вже побував на ній. Розглянемо, як можна не будувати граф, але розв’язати задачу за допомогою того ж самого алгоритму. Якщо уважно подивитись на шахівницю, можна побачити, що з будь-якої клітинки кінь може стрибнути не більш ніж на 8 клітинок (див. малюнок). Якщо (i,j) – координати коня, то клітинки, на яких кінь може опинитись через один хід, мають такі координати (звичайно, якщо вони існують, тобто кінь не виходить за межі шахівниці): (i-2,j-1), (i-2,j+1), (i+2,j-1), (i+2,j+1), (i-1,j-2), (i-1,j+2), (i+1,j-2), (i+1,j+2). Отже, немає сенсу перебирати всі клітинки шахівниці, щоб знайти продовження шляху коня. Також відпадає необхідність зберігати матрицю суміжності (або список ребер графа). У стеку можна зберігати лише напрямок руху коня, якщо значення перевищує 8, шляхи вичерпано. Щоб запам’ятати сам шлях коня, зберігатимемо відвідані клітинки у таблиці шлях, а щоб не потрапити знову в ту саму клітинку, напишемо на відповідній клітинці номер ходу, якщо клітинку вже відвідано, та 0, якщо ні.
Запишемо постановку задачі для пошуку маршруту коня. Алг Шлях_Коня(Ціл m,n, Ціл Таб шлях [1..2, 1..m*n]) Арг m,n Рез шлях Нагадуємо, що якщо шлях коня існує, він містить усі клітинки шахівниці, причому кожна клітинка зустрічається у шляху рівно один раз. Тому, щоб прискорити перевірку, чи побував кінь на деякій клітинці, оголосимо хеш-таблицю дошка [1..m, 1..n], у кожну комірку якої записуватимемо номер ходу, якщо кінь побував на відповідній клітинці, або нуль, якщо кінь ще не побував на ній. Отже, маємо таку структуру даних Алг Шлях_Коня(Ціл m,n, Ціл Таб шлях [1..2, 1..m*n]) Арг m,n Рез шлях Поч Ціл Таб стек[0..m*n], дошка[1..m, 1..n] Ціл вказ Кін У стеку зберігаємо номер напрямку ходу коня (від 1 до 8). Якщо кінь може зробити хід, записуємо номер ходу в таблицю "дошка", координати кілтинки до результату (таблиці "шлях") і переходимо до наступного ходу. Якщо кінь не може зробити хід, переходимо до наступного напрямку, якщо всі напрямки вичерпано - скасовуємо останній хід, записуємо 0 у таблицю "дошка" і повертаємось назад. Початковою клітинкою може бути будь-яка, наприклад, (1, 1). Зауважимо, що якщо m,n>3, шлях коня з клітинки (1, 1) існує (крім шахівниці 4*4, для якої не існує жодного шляху коня). Якщо m=3, шлях коня існує при n=4, n>6. Алг Шлях_Коня(Ціл m,n, Ціл Таб шлях [1..2, 1..m*n])Арг m,n Рез шлях Поч Ціл Таб стек[0..m*n], дошка[1..m, 1..n] Ціл вказ Лог знайдено_маршрут Обнулити стек вказ:=1 записати у шлях початкову клітинку знайдено_маршрут:=хибне Повтори Повтори стек[вказ]:=стек[вказ]+1 до стек[вказ]>8 або ставимо_коня Якщо стек[вказ]<=8 то запам'ятати нову клітинку вказ:=вказ+1 інакше вилучити останню клітинку все Якщо вказ=m*n то знайдено_маршрут:=істина вказ:=вказ-1 все до вказ=0 або знайдено_маршрут Кін
Для деталізації алгоритму з'ясуємо, що значить "ставимо_коня". Відомий напрямок руху коня - один з восьми можливих. Для того, щоб хід був можливим, необхідно, по-перше, клітинка існувала, по-друге, була вільною. Реалізувати цю перевірку зручно, використовучи допоміжний алгоритм-функцію з побічним ефектом - координати клітинки, у якій опиниться кінь після вдалого ходу. Лог Алг ставимо_коня (Ціл напр, х, у, х1, у1) Арг напр, х, у Рез х1, у1 Зручно викликати цей допоміжний алгоритм так, щоб у випадку вдалого ходу результат записувався до таблиці "шлях". Нагадуємо, що напрямок записано у верхівці стеку. х, у - координати коня в кінці шляху, х1, у1 - координати, в яких кінь опиниться після вдалого ходу, напр - напрямок ходу коня (один з восьми можливих).
Лог Алг ставимо_коня (Ціл напр, х, у, х1, у1) Арг напр, х, у Рез х1, у1 Поч Вибір при напр=1 х1:=х-2 у1:=у-1 при напр=2 х1:=х-2 у1:=у+1 при напр=3 х1:=х+2 у1:=у-1 при напр=4 х1:=х+2 у1:=у+1 при напр=5 х1:=х-1 у1:=у-2 при напр=6 х1:=х-1 у1:=у+2 при напр=7 х1:=х+1 у1:=у-2 при напр=8 х1:=х+1 у1:=у+2 все Знач:= x1>=1 та х1<=m та y1>=1 та у1<=n та дошка[x1, y1]=0 Кін Наводимо головний алгоритм Алг Шлях_Коня(Ціл m,n, Ціл Таб шлях [1..2, 1..m*n]) Арг m,n Рез шлях Поч Ціл Таб стек[0..m*n], дошка[1..m, 1..n] Ціл вказ Лог знайдено_маршрут Обнулити стек вказ:=1 шлях[1,1]:=1 {записуємо початкову клітинку} шлях[2,1]:=1 знайдено_маршрут:=хибне Повтори Повтори стек[вказ]:=стек[вказ]+1 до стек[вказ]>8 або ставимо_коня(стек[вказ], шлях[1,вказ], шлях[2,вказ], шлях[1,вказ+1], шлях[2,вказ+1]) Якщо стек[вказ]<=8 то дошка[шлях[1,вказ], шлях[2,вказ], ]:=вказ {запам'ятати нову клітинку} вказ:=вказ+1 інакше дошка[шлях[1,вказ], шлях[2,вказ], ]:=0 {вилучити останню клітинку} стек[вказ]:=0 вказ:=вказ-1 все Якщо вказ=m*n то знайдено_маршрут:=істина дошка[шлях[1,вказ], шлях[2,вказ], ]:=0 {вилучити останню клітинку}стек[вказ]:=0 вказ:=вказ-1 все до вказ=0 або знайдено_маршрут Кін Зауваження. Якщо не використовувати змінну знайдено_шлях, алгоритм знаходить всі можливі маршрути коня, що починаються у певній клітинці. Наведений алгоритм ще називають пошуком з поверненням, тому що у процесі пошуку відбувається повернення до вже відвіданої позиції. У даній задачі це клітинка, в якій знаїодиться кінь. Звичайно, за допомогою такої стратегії можна розв'язувати багато задач. Відрізнятимуться розв'язки тільки перевіркою умови "йти далі чи повертатись назад", а також перевіркою, чи знайдено розв'язок. |