|
Алгоритм знаходження всіх маршрутів у простому графі. Минулого уроку розглядався процес обходу простого графа з метою знаходження всіх маршрутів заданої довжини з початкової вершини. Маршрут у графі - це певна послідовність вершин, яку можна зберігати як лінійну таблицю. Необхідно також пам'ятати кількість заповнених комірок, тобто довжину знайденого маршруту. Отримаємо таку структуру даних: Алг Пошук_маршрутів(Ціл s, L, n , Ціл Таб a[1..n,1..n]) Арг s, L, n, a Поч Ціл Таб стек[0..L] Ціл вказ Кін Надалі називатимемо Ціл Таб стек[0..L] стеком, а вказ - вказівником стеку. стек[вказ] - верхівка стеку. Зручно, коли значення вказівника дорівнює кількості ребер у маршруті. Якщо вершину ще не додано, у відповідній комірці записуватимемо нульове значення. Яке значення на початку пошуку доцільно надати змінній "вказ"?
Зауважимо, що в комірці 0 таблиці "стек" завжди записана початкова вершина. Оскільки алгоритм на кожному кроці передбачає, що стек містить коректний шлях, при доповненні маршруту новою вершиною немає сенсу перевіряти весь список, чи утворює він маршрут - достатнью перевірити останню пару, чи суміжні вершини, що її утворюють. Можливі два випадки - або нова вершина суміжна з останньою, або ні. Якщо так, дописуємо нову вершину до маршруту. Якщо ж ні, шукатимемо іншу. Якщо вдалося підібрати вершину, що продовжує шлях, і при цьому ще не отримано маршрут потрібної довжини, продовжуємо побудову маршруту, якщо отримано - виводимо отриманий маршрут і шукатимемо наступний.
Як дописати наступну вершину до стеку?
Деталізуємо алгоритм Пошук_маршрутів. Алг Пошук_маршрутів(Ціл s, L, n , Ціл Таб a[1..n,1..n]) Арг s, L, n, a Поч Ціл Таб стек[0..L] Ціл вказ Обнулити стек стек[0]:=s {початкова вершина} вказ:=1 Повтори Знайти маршрут довжиною L і надрукувати його До більше немає маршрутів Кін Щоб зберегти лексикографічний порядок генерації маршрутів, завжди будемо дописувати до вже знайденого маршруту вершину з мінімально можливим номером. Розглянемо приклад з минулого уроку. Нехай необхідно знайти всі маршрути довжиною 3 ребра, що починаються у вершині 4 у графі, зображеному на малюнку. 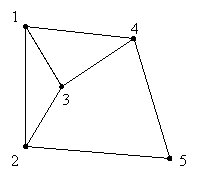 Мінімальна вершина (вершина з мінімальним номером), яку можна додати до маршруту - це перша. Нагадаємо, що вказівник містить значення 1, а у відповідній комірці записано нульове значення. Щоб підібрати вершину, яка продовжує маршрут і яка має мінімально можливий номер, збільшуватимемо значення верхівки стеку на 1. Наприклад, якщо початкова вершина ізольована, підібрати суміжну з нею неможливо. В іншому випадку у верхівці стеку повинен опинитись шуканий номер вершини. Нагадаємо, що якщо вершина не підходить, тому що не суміжна з останньою раніше записаною до стеку, переходимо до наступної. Зауважимо, що можна використати і цикл з передумовою, але краще застосувати саме цикл з післяумовою, тому що записане у верхівці стеку значення зміниться хоча б один раз. Алг Пошук_маршрутів(Ціл s, L, n , Ціл Таб a[1..n,1..n]) Арг s, L, n, a Поч Ціл Таб стек[0..L] Ціл вказ Обнулити стек стек[0]:=s {початкова вершина} вказ:=1 Повтори Повтори стек[вказ]:=стек[вказ]+1 До знайдено нову вершину або з'ясовано, що вершини не існує До більше немає маршрутів Кін Після виходу з внутрішнього циклу можливі тільки два випадки. Якщо знайдено продовження маршруту, переходимо до пошуку наступної вершини. Для цього потрібно просто збільшити на 1 верхівку стеку. Після цього процес пошуку наступної вершини повторюється. Шкільною алгоритмічною мовою цей випадок можна записати так. Якщо стек[вказ]<=n то вказ:=вказ+1 інакше все Для прикладу, наведеному вище, отримаємо 4-1, потім 4-1-2, потім 4-1-2-1. Взагалі, в момент знаходження чергового маршруту значення вказівника перевищує розмір стеку. В такому випадку виводимо знайдений маршрут і повертаємо вказівник на одну позицію назад, тобто на останню вершину, яка записана у стеку. Це необхідно для знаходження наступних шляхів. Запишемо ці дії шкільною алгоритмічною мовою. Алг Пошук_маршрутів(Ціл s, L, n, Ціл таб a[1..n,1..n]) Арг s, L, n, a Поч Ціл таб стек[0..L] Ціл вказ Обнулити стек стек[0]:=s {початкова вершина} вказ:=1 Повтори Повтори стек[вказ]:=стек[вказ]+1 до стек[вказ]>n або суміжні(стек[вказ], стек[вказ-1]) Якщо стек[вказ]<=n то вказ:=вказ+1 інакше все Якщо вказ>L то друк стеку вказ:=L все до більше немає маршрутів Кін Виконуючи написаний алгоритм, отримаємо маршрут 4-1-2-1, За ним 4-1-2-3, потім 4-1-2-5. Легко побачити, що більше не існує маршрутів довжини 3, що починаються 4-1-2. У цьому випадку необхідно обнулити верхівку стеку і перейти до попередньої комірки (тобто вилучити зі стеку неіснуючу вершину). Коли ж стек виявиться порожнім, алгоритм закінчує свою роботу. Алг Пошук_маршрутів(Ціл s, L, n , Ціл Таб a[1..n,1..n]) Арг s, L, n, a Поч Ціл Таб стек[0..L] Ціл вказ Обнулити стек стек[0]:=s {початкова вершина} вказ:=1 Повтори Повтори стек[вказ]:=стек[вказ]+1 до стек[вказ]>n або суміжні(стек[вказ], стек[вказ-1]) Якщо стек[вказ]<=n то вказ:=вказ+1 інакше стек[вказ]:=0 вказ:=вказ-1 все Якщо вказ>L то друк стеку вказ:=L все до вказ=0 Кін |
