|
Дерево пошуку. Розглянемо задачу, яку можна розв'язувати за допомогою пошуку в глибину, але яка дещо відрізняється від задач, запропонованих на минулих уроках. Задача про переливання. Є посудина, яка вміщує рівно N літрів рідини. За один хід можна долити А або В літрів. Доливати можна тільки в тому випадку, якщо у посудині ще є місце для такого об'єму. Також можна виливати з посудини А або В літрів, якщо такий об'єм рідини є в посудині. Спочатку посудина порожня. Вказати спосіб наповнення посудини за мінімальну кількість переливань. Доливання позначатимемо +А, виливання відповідно -А. Розглянемо приклади. N=10, А=2, В=4. Шукана послідовність переливань +2+4+4. N=10, А=7, В=4. Маємо такий спосіб: +7-4+7. Спроектуємо алгоритм для розв'язання задачі пошуком у глибину. Слід лише врахувати, що заздалегідь кількість переливань невідома. Існує ще один дуже важливий аспект. Об'єм рідини у посудині не повинен повторюватись. Дійсно, якщо у якісь різні моменти часу в посудині була одна й та сама кількість рідини, ці переливання можна просто вилучити. Якщо це не врахувати, алгоритм пошуку в глибину зациклиться. При реалізації мовою Паскаль завершить роботу помилкою виконання, тому що фізичний об'єм пам'яті обмежений. Отож, у процесі пошуку перевірятимемо, чи зустрічалась раніше кількість рідини. Якщо так, переливання вважатимемо таким, що не є продовженням послідовності. Кодуємо +А числом 1, +В – числом 2, відповідно –А та –В – числами 3 і 4. Для зберігання об’ємів, які вже зустрічались, використовуємо множину. У всьому іншому алгоритм будується аналогічно до задачі “Обхід конем”. Зауважимо, що наведений алгоритм знаходить усі способи переливань. Вибрати найкоротший пропонується самостійно.
Алг Переливання1 (ціл n,a,b) Арг n,a,b Поч ціл таб стек[1..n] ціл x,y множ m {об'єми, що вже зустрічались} x:=0 {початковий об'єм рідини} Обнулити стек вказ:=1; {перше переливання} m:=[0]; {порожня посудина} повтори повтори стек[вказ]:= стек[вказ]+1; до (стек[вказ]>4) або можливо(стек[вказ],x,y); якщо стек[вказ]<=4 {переливання можливе} то якщо y=n {посудину наповнено} то надрукувати спосіб заповнення інакше {посудину не наповнено} x:=y; {новий об'єм рідини} m:=m+[x]; {вже зустрічався} вказ:=вказ+1; все інакше {переливання неможливе} s[вказ]:=0; {вилучаємо з верхівки стеку} m:=m-[x]; {об'єм рідини} вказ:=вказ-1; вибір {відновлюємо попередній об'єм рідини} при стек[вказ]=1 x:=x-a; при стек[вказ]=2 x:=x-b; при стек[вказ]=3 x:=x+a; при стек[вказ]=4 x:=x+b; все все все до вказ=0 Кін
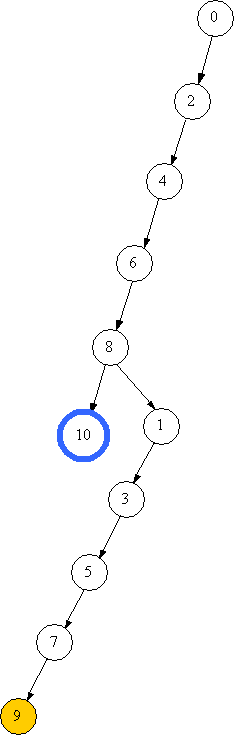
Лог алг function можливо(ціл k,x,z) Арг k,x Рез z { k - верхівка стеку, x - початковий об'єм, z - кінцевий об'єм} поч вибір {в залежності від способу переливання} при k=1 { знаходимо новий об'єм} z:=x+a; при k=2 z:=x+b; при k=3 z:=x-a; при k=4 z:=x-b все знач:=(z>0) і (z<=n) і (z не належить m) {не виходимо за межі посудини та об'єм не зустрічався раніше} кін Зображатимемо стан посудини (об’єм рідини) та переливання на малюнках. Отже, початковий стан – “0”. Переливання +2 (долити 2) можливе, тому що 2 менше за 10 і стан 2 ще не зустрічався. Зі стану 2 можна перейти до стану 4, потім до стану, 6, 8, 10. Поточний стан на малюнках виділено.  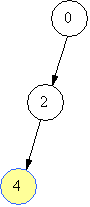 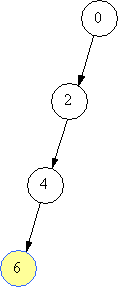 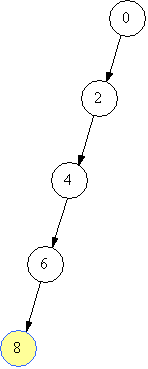 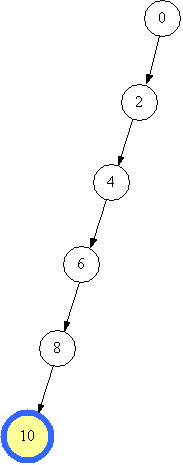 Але чи є знайдений спосіб оптимальним за кількістю переливань? Це залежить від вхідних даних. Зауважимо, що не завжди можна отримати спосіб переливання відразу. Наприклад, якщо взяти а=3, то отримаємо 3, 6, 9, а далі? Посудину не наповнено, а долити 3 не можна, бо 9+3=12 більше за 10. В таких випадках необхідно повернутись до попереднього стану і шукати інше продовження. Повертаємось тепер до нашого прикладу. Отже, шукаємо інший варіант продовження переливань від стану 8. Перехід “+7” неможливий, тому що 8+7=15 більше за 10, перехід “-2” неможливий, тому що призведе до стану 6, а 6 вже було. Перехід “-7” можливий, призведе до стану 1. 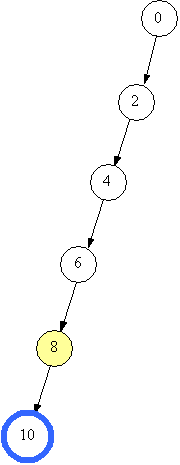
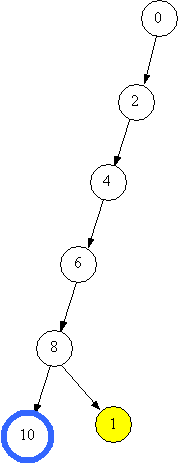 Виконуємо алгоритм далі. Переходимо від стану 1 до станів 3, 5, 7 та 9.
Стан 9 – це глухий кут, бо жодного переливання, яке призводить до нового стану, не існує. Дійсно, 9+2=11 та 9+7=16: долити у посудилу, що містить 9 літрів, ні 2, ні 7 літрів неможливо. Якщо ж вилити 2, отримаємо стан 7, а якщо вилити 7, отримаємо 2. В обох випадках стан посудини вже зустрічався. Тому повертаємось до стану 7. Стан 7 – теж глухий кут, тому що +7 - неможливо, -2 та -7 призводять до повторення. Отже, повертаємось до стану 5. Отже, переходимо до стану 3. Переливання 3+2 вже розглянуто повністю, наступний перехід 3+7=10 призведе до мети – посудину заповнено. Знайдено другий спосіб заповнення посудини. 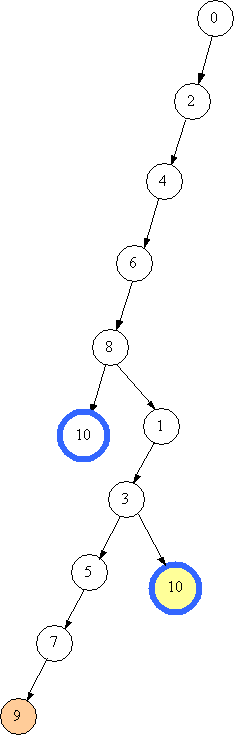
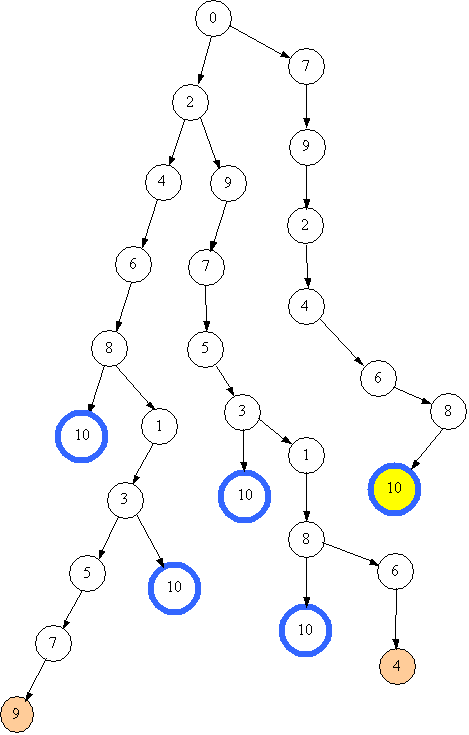
Уважний читач може помітити, що другий спосіб заповнення довший за перший. Дійсно, якщо раніше було знайдено спосіб заповнити посудину за 5 переливань, не варто навіть розглядати 6 та більше. Ця ідея є основною при реалізації відсікання перебору і називається методом гілок і границь. Наведений алгоритм неважко вдосконалити, якщо запам’ятати знайдену кількість переливань, а стан, що досягнуто за цю кількість, відмінний від цільового, вважати глухим кутом. Отже, повертаємось до стану 3. Переходи “-2” та “-7” зі стану 3 неможливі, повертаємось до 1. Зі стану “1” переходи “+7”, “-2” та “-7” також неможливі, повертаємось до 8. Усі можливі переливання для цього стану вже розглянуто, переходимо до 6. З 6 стану переходи “+7”, “-2” та “-7” неможливі, переходимо до 4, аналогічно переходимо до 2. Наведені малюнки утворюють дерево пошуку розв'язків задачі. Круги на малюнку вважаються вузлами і відповідають станам посудини, стрілки вважаються гілками і відповідають переходам (в нашій задачі переливанням). Зауважимо, що дерево пошуку згідно наведеного алгоритму будується зверху вниз. Саме тому ця стратегія і отримана таку назву - пошук в глибину. Продовжиму будувати дерево для даної задачі. 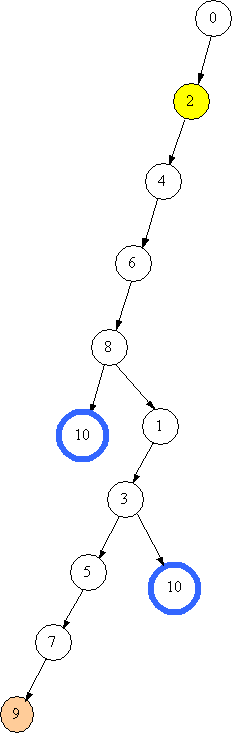 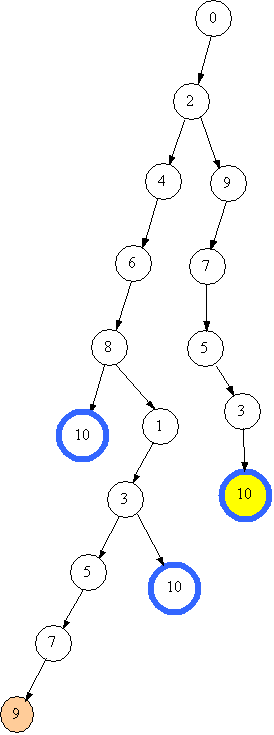
Отже, від третього розв'язку (тобто зі стану 10) повертаємось до попереднього стану, а далі переходимо від стану 3 до стану 1. На малюнках показано наступні кроки, що призводять до знаходження четвертого розв'язку. 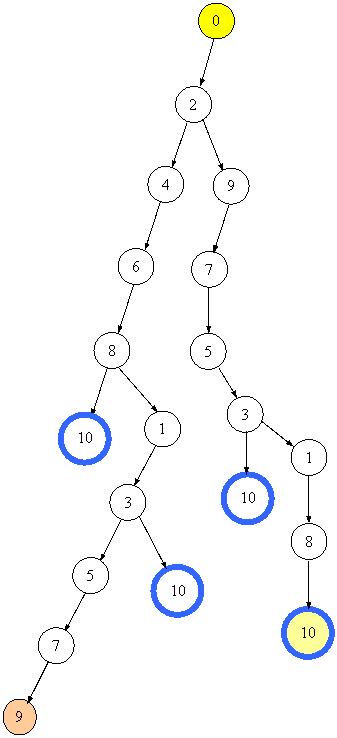 Після знаходження четвертого розв'язку повертаємось до стану 8.
Отже 4 - глухий кут.
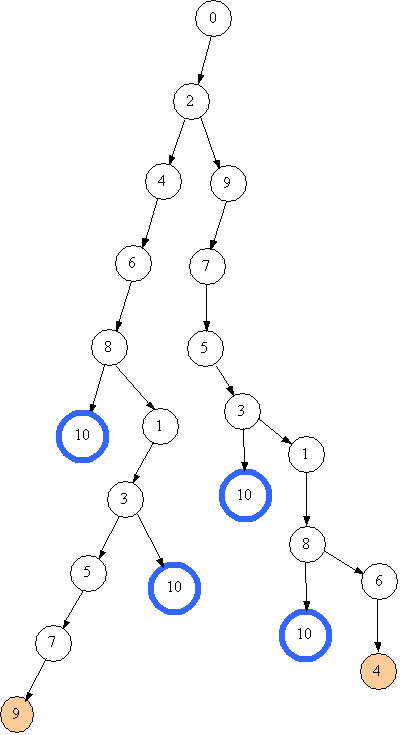 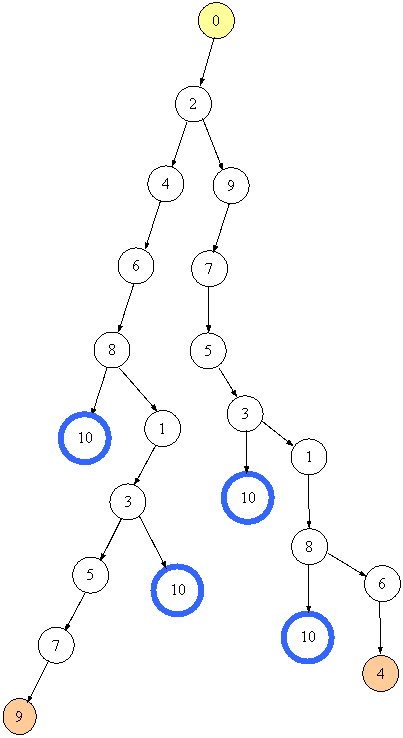 Таким чином, вичерпано всі варіанти щодо першого переливання +2, і потрібно переходити до першого переливання +7. На наступному малюнку показано процес отримання п'ятого розв'язку.
Після повернення до стану 8 переходимо до стану 1. Далі отримуємо 3, потім 5 і знову глухий кут. Зі стану 5 неможливо перейти до будь-якого іншого. 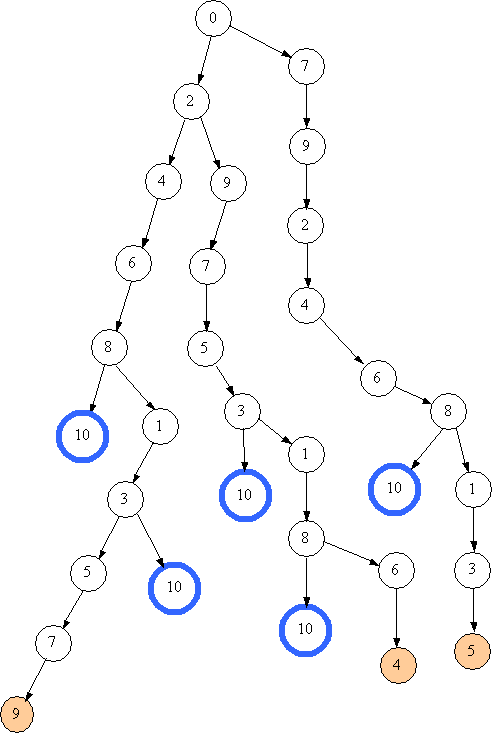 Повертаємось на 3, перехід 3+7 дає шостий розв'язок.
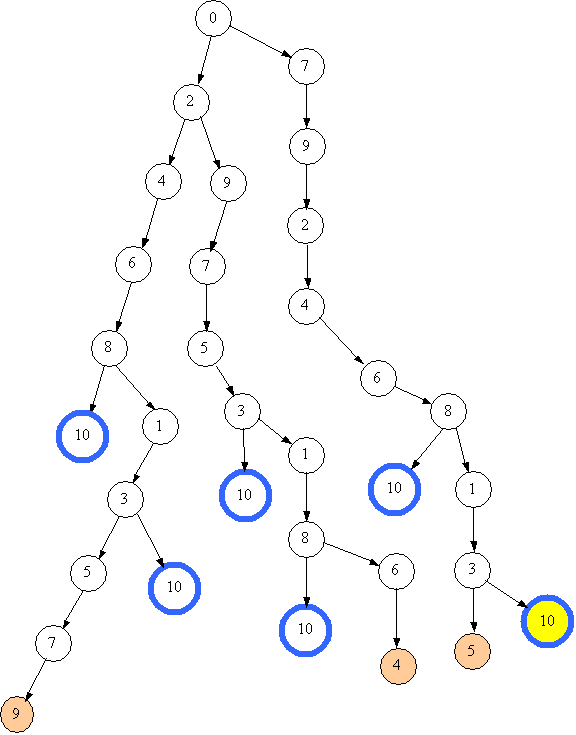 Повертаємось назад. Наступний вузол, з якого можна утворити нову гілку, має номер 7. Тобто переходимо аж до першого переливання. На наступному малюнку наведено проце отримання сьомого розв'язку. 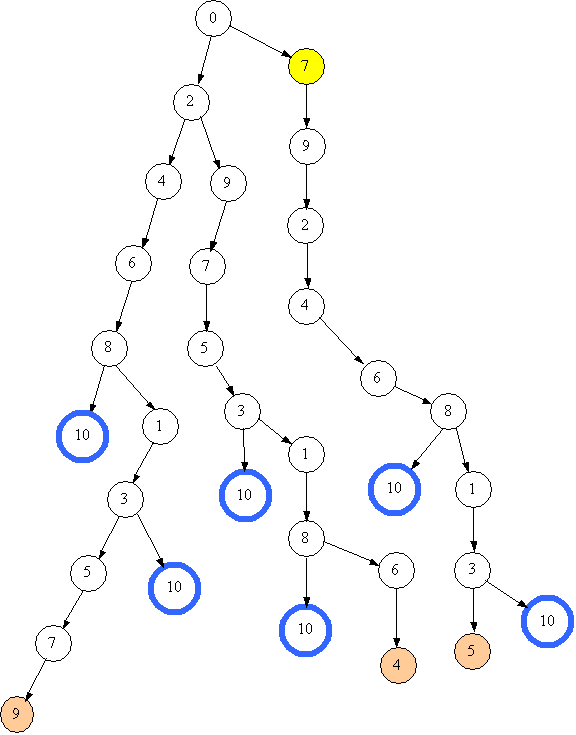 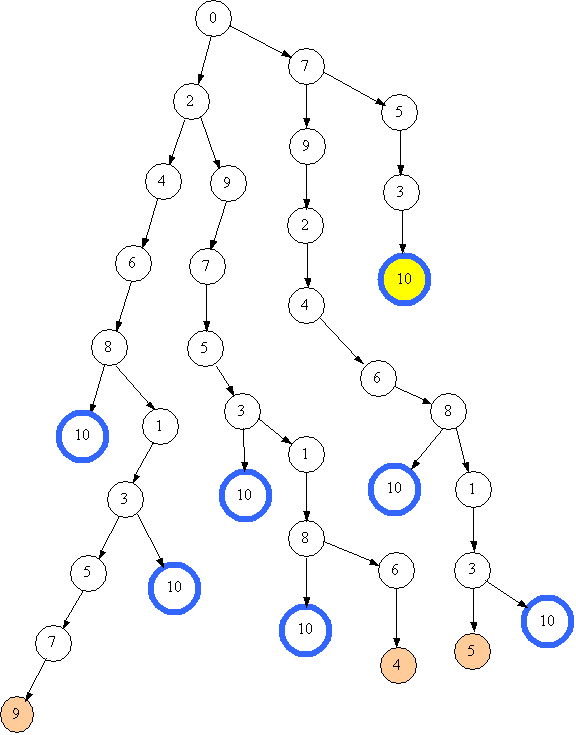 Сьомий розв'язок виявився кращим з всі попередні - всього 4 переливання. Але чи є він оптимальним? Подивимось, як утворюється восьмий розв'язок. 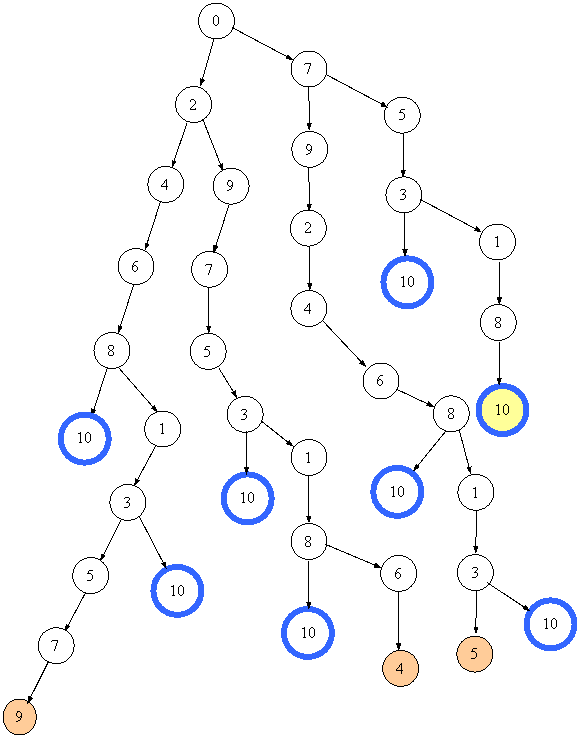 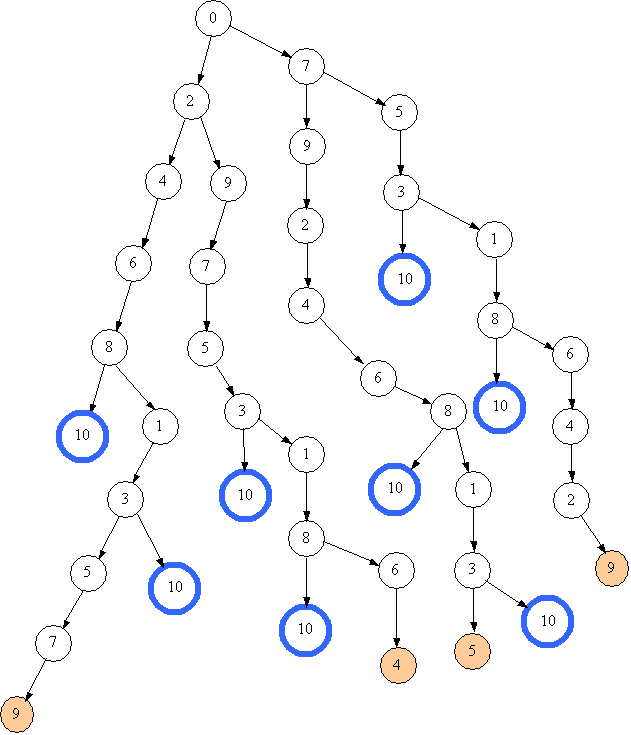 Повернення від глухого кута відбувається до стану 0, а оскільки більше нічого зі стану 0 не можно утворити, алгоритм завершує свою роботу. Підведемо підсумки. Знайдено 8 різних способів наповнити посудину, сьомий виявився оптимальним. Побудовано повне дерево пошуку. |