Коды, коды, коды.Выбор псевдослучайной кодовой последовательности в радиотехнической системе передачи информации очень важен, поскольку от ее параметров зависит усиление обработки системы, ее помехоустойчивость, чувствительность. При одной и той же длине кодовой последовательности, параметры системы могут быть различны. Системы, использующие сложные шумоподобные сигналы, применяются уже более 50 лет. Известные достоинства шумоподобных сигналов, такие как высокая помехозащищенность по отношению к узкополосным помехам большой мощности, возможность разделения абонентов по кодовому признаку, скрытность передачи, высокая устойчивость к многолучевому распространению и даже высокая разрешающая способность при радиолокационных и навигационных измерениях, предопределили их использование в различных системах связи и определения местоположения. За счет каких параметров шумоподобных сигналов их применение обладает рядом чудесных свойств и можно ли их улучшить? Характеристики шумоподобных сигналов Важным параметром системы, использующей шумоподобные сигналы, является выигрыш при обработке (processing gain). Выигрыш при обработке (ВО) показывает степень улучшения отношения сигнал/шум при преобразовании полученного приемником шумоподобного сигнала в требуемый информационный сигнал. Эта процедура получила название сжатия или дераспределения (despreading). Согласно классическому определению, ВО равен: ВО = 10 Lg [Ск /Си], где Ск – частота следования чипов псевдослучайной последовательности, чип/секунду. Си – скорость передачи информации, бит/секунду. По этому определению система, которая имеет скорость передачи информации 1 Мбит/секунду и частоту следования чипов 11 Мчип/секунду (это означает, что каждый бит информации кодируется псевдослучайной последовательностью из 11 битов), будет иметь ВО, равный 10,41 дБ. Этот результат означает, что работоспособность системы передачи информации сохранится с тем же коэффициентом BER, если полезный сигнал на входе уменьшится на 10,41 дБ. В обычных коммерческих шумоподобных радиомодемах, таких как Arlan, Wavelan, и им подобных, наибольшее значение зачастую уделяется скорости передачи информации, а не скрытности или помехоустойчивости. Поскольку инструкциями федеральной комиссии по связи в США (FCC) для таких устройств предусмотрено минимальное значение ВО 10 дБ, а также выделена минимально допустимая ширина полосы частот одного канала (что накладывает ограничения на максимальную частоту следования чипов Ск), то длина псевдослучайной кодовой последовательности должна быть не менее 11 чипов на бит. Если, увеличить длину кодовой последовательности до 64 чипов на бит (это максимально возможная длина для широкоизвестного процессора ШПС Z87200 фирмы Zilog), то при той же частоте следования чипов 11 Мчип/секунду, выигрыш при обработке будет 10Lg (64) = 18,06 дБ, скорость передачи информации при этом уменьшится в 64/11 = 5,8 раза. Чтобы быть использованными в ШПС системе, кодовые последовательности должны обладать определенными математическими и другими свойствами, основными из которых являются очень хорошие автокорреляционные и взаимокорреляционные свойства. Кроме того, кодовая последовательность должна быть хорошо сбалансирована, то есть число единиц и нулей в ней должно отличаться не более чем на один символ. Последнее требование важно для исключения постоянной составляющей информационного сигнала. DSSS приемник сравнивает полученную кодовую последовательность с точной ее копией, хранящейся в памяти. Когда он обнаруживает корреляцию между ними, то переходит в режим приема информации, устанавливает синхронизацию и начинает операцию декодирования полезной информации. Любые частичные корреляции могут привести к ложному срабатыванию и нарушению работы приемника, вот почему кодовая последовательность должна обладать хорошими корреляционными свойствами. Рассмотрим понятие корреляции более подробно. Автокорреляционная и взаимокорреляционная функция Корреляционные свойства кодовых последовательностей, используемых в ШПС системах, зависят от типа кодовой последовательности, ее длины, частоты следования ее символов и от ее посимвольной структуры.(1). В общем виде автокорреляционная функция (АКФ) определяется интегралом: Y (t ) = ∫f(t)f(t-t )dt и показывает связь сигнала с копией самого себя, смещенного во времени на величину τ. Изучение АКФ играет важную роль при выборе кодовых последовательностей с точки зрения наименьшей вероятности установления ложной синхронизации. Взаимокорреляционная функция (ВКФ), с другой стороны, имеет большое значение для систем с кодовым разделением абонентов, таких как CDMA, и отличается от АКФ только тем, что под знаком интеграла стоят разные функции, а не одна и та же: Y (t ) = ∫f(t)g(t-t )dt ФКВ показывает, таким образом, степень соответствия одной кодовой последовательности другой. Чтобы упростить понятия АКФ и ВКФ можно представить значение той или иной функции как разность между числом совпадений А и несовпадений Б символов кодовых последовательностей при их посимвольном сравнении. Для иллюстрации этого примера, рассмотрим автокорреляционную функцию кодовой последовательности Баркера длиной 11 чипов, имеющей следующий вид: 1 1 1 0 0 0 1 0 0 1 0 Посимвольное сравнение этой последовательности с ее же копией сведем в таблицу.
Графическое изображение АКФ данной последовательности Баркера показано на рисунке: 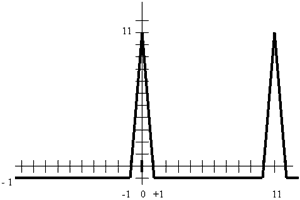
Такую АКФ можно назвать идеальной, поскольку на ней отсутствуют боковые пики, которые могли бы способствовать ложному обнаружению сигнала. В качестве негативного примера можно рассмотреть любую произвольную кодовую последовательность, например: 1 1 1 0 0 0 1 1 1 0 0 Проведя соответствующие предыдущему примеру вычисления, получим следующее графическое изображение автокорреляционной функции, показанное на рисунке: 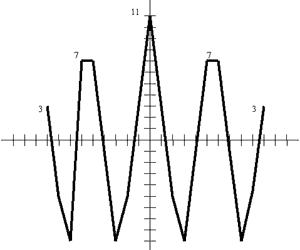
Боковые пики величиной 7 и 3 единиц могут привести к ложному срабатыванию системы в случае применения такой последовательности для распределения сигнала. Для высокоскоростных ШПС систем, предназначенных для передачи информации, но не для кодового разделения абонентов, обычно используются коды Баркера, обладающие хорошими автокорреляционными свойствами. С помощью компьютерного моделирования были найдены так называемые коды Уилларда (2), которые при той же длине, что и коды Баркера, обладают иногда лучшими корреляционными свойствами. Кодовые последовательности Баркера, имеющие длину более 13 символов, неизвестны, поэтому для получения большего ВО, большей помехоустойчивости, а также для кодового разделения абонентов, используют последовательности большей длины, значительную часть которых образуют М-последовательности. М-последовательности Одним из самых известных фазоманипулированных сигналов являются сигналы, кодовые последовательности которых являются последовательностями максимальной длины или М-последовательности. Для построения М-последовательностей обычно используют регистры сдвига или элементы задержки заданной длины. Длина М-последовательности равна 2N-1, где N – число разрядов регистра сдвига. Различные варианты подключения выходов разрядов к цепи обратной связи дают некоторый набор последовательностей. АКФ М-последовательности равна –1 для всех значений задержки, кроме области 0±1, где ее значение меняется от –1 до значения 2N-1. Кроме того, М-последовательности обладают еще одним интересным свойством: в каждой последовательности единиц на одну больше, чем нулей. Способам формирования и характеристикам М-последовательностей посвящено много литературы, поэтому мы не будем останавливаться на этом подробно. Для исследования возможностей нового комплекта микросхем PRISMTM фирмой Harris Semiconductor было проведено практическое исследование коротких М-последовательностей и кодов Баркера с целью нахождения оптимальных из них с точки зрения автокорреляционной функции (3). В рамках этого исследования была проанализирована М-последовательность длиной 15 и имеющая вид: 111 1000 1001 1010 Как выяснилось, она обладает худшими автокорреляционными свойствами, чем последовательность Баркера длиной 13 символов следующего вида: 1 1111 0011 0101 Практический вид АКФ М-последовательности показан на рисунке: 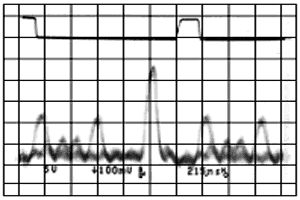
Для сравнения, АКФ кодовой последовательности Баркера длиной 13: 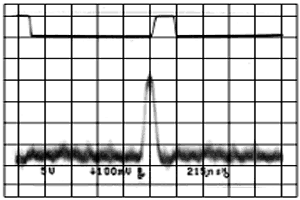
Сверху на фотографии показан синхроимпульс осциллографа. Как видно из фотографий, М-последовательность имеет несколько больших боковых пиков, которые могут значительно ухудшить приемные качества ШПС системы, а иногда может привести к ложному обнаружению сигнала. Как оказалось в процессе дальнейших исследований, если к 13 символьной кодовой последовательности Баркера добавить два нуля, то АКФ полученной последовательности 001 1111 0011 0101 будет значительно лучше, чем описанная АКФ М-последовательности, состоящей также из 15 символов. АКФ вновь полученной последовательности: 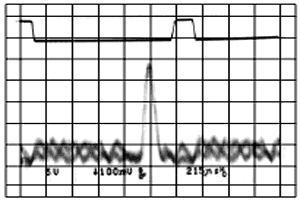
Короткие М-последовательности таким образом значительно уступают последовательностям Баркера по автокорреляционным свойствам, несмотря на лучший баланс нулей и единиц. Из наиболее известных систем, использующих М-последовательности, можно назвать подвижную систему связи с кодовым разделением абонентов CDMA и систему глобальной навигации GPS. В системе CDMA используются три кодовых последовательности. Первая из них, используемая для синхронизации работы всего оборудования, обладает переменной длиной N ≈ (32÷131)103 символов. Вторая М-последовательность обладает максимальной длиной N=242-1 и используется для идентификации абонентских станций со стороны базовой станции. Третья последовательность используется для передачи полезной информации между базовой и абонентской станциями и представляет собой одну из последовательностей Уолша. Последовательности Уолша (в качестве них выступают строки или столбцы матрицы Адамара) обладают свойством ортогональности по отношению друг к другу. С математической точки зрения ортогональность означает, что при отсутствии временного сдвига между последовательностями Уолша, их скалярное произведение равно нулю. С точки зрения радиотехнической, это позволяет устранить взаимные помехи при передаче информации от базовой станции к нескольким абонентским и тем самым резко повысить пропускную способность системы связи (5). Данное преимущество ортогональности имеем место только в случае точной синхронизации передачи последовательностей всем абонентам. Точная синхронизация базовых и абонентских станций CDMA осуществляется главным образом с помощью глобальной навигационной системы GPS. Кроме последовательностей Уолша в системах связи используются другие ортогональные последовательности: последовательности Диджилок и Стиффлера. Кроме М-последовательностей как таковых в системах связи нашли применения составные кодовые последовательности, представляющие собой комбинации М-последовательностей и обладающие некоторыми специфическими свойствами. Наиболее известными и применяемыми из них являются последовательности Гоулда. Кодовые последовательности Гоулда формируются с помощью простого генератора последовательностей на основе двух регистров сдвига одинаковой разрядности и обладают по отношению к М-последовательностям двумя достоинствами. Во-первых, генератор кодовых последовательностей, построенный на основе двух регистров сдвига длиной N каждый, может генерировать кроме двух исходных М-последовательностей еще N последовательностей длиной 2N-1, то есть значительно расширяется число генерируемых кодовых последовательностей. Во-вторых, коды Гоулда могут быть выбраны так, что ВКФ для всех получаемых от одного генератора кодовых последовательностей будет одинаковой, а величина ее боковых пиков ограничена. Для М-последовательностей нельзя гарантировать, что боковые пики ВКФ не будут превосходить определенную заданную величину. Кодовые последовательности Гоулда применяются в глобальных системах навигации, например в GPS. Так называемый “грубый” код (C/A – clear/acquisition) использует последовательность Гоулда длиной 1023 символа, передающуюся с тактовой частотой 1,023 МГц. Точный же код (P - precision), доступ к которому имеют военные и специальные службы, использует сверхдлинную составную последовательность с периодом повторения 267 дней и тактовой частотой 10,23 МГц. Кроме составных последовательностей Гоулда наиболее часто применяются последовательности Касами. |
