|
Пошук маршрутів заданої довжини у простих графах. Нехай задано простий граф, початкова вершина s та довжина маршруту L. Необхідно знайти всі маршрути довжиною L, що починаються у вершині s. Напишемо постановку задачі. Алг Пошук_маршрутів(ціл s, L, n , ціл таб a[1..n,1..n]) Арг s, L, n, a Тут n - кількість вершин графа, a - його матриця суміжності. Результат - всі можливі маршрути, що відповідають умові. Кількість шуканих шляхів заздалегідь невідома, тому можна описати структуру даних для зберігання всіх маршрутів як Ціл таб z[1..k, 0..L], де k - кількість знайдених маршрутів. Але для не дуже великих графів k зростає надзвичайно швидко (так званий комбінаторний вибух). Тому ми не будемо зберігати всі маршрути в пам'яті, а виводитимемо їх по мірі знаходження. Розглянемо приклад. 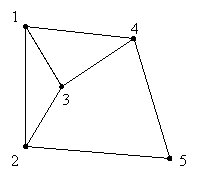 Нехай необхідно знайти всі маршрути довжиною 3 ребра, що починаються у вершині 4. Для того, щоб перерахувати всі маршрути, опишемо лексикографічний порядок, згідно якого маршрут, друга вершина якого має менший номер, повинен бути отриманий раніше, якщо друга вершина одна й та сама, то раніше отримується маршрут, у якого третя вершина має менший номер. І так далі, до останньої вершини. Зауважимо, що якщо маршрут деякої довжини знайдено, то його можна продовжити шляхом додавання вершин у кінець у випадку, коли вершина, що додається, суміжна з останньою у маршруті. Якщо вершина, що додається, не суміжна з останньою у маршруті, отримана послідовність вершин не утворюватиме маршрут. Отже, для знаходження першого маршруту необхідно щоразу вибирати вершину з мінімальним номером. Всі маршрути у графі можна знайти за такою стратегією. Спочатку знаходимо перший маршрут (у лексикографічному порядку). Далі за першим маршрутом знаходимо другий, за другим - третій і так далі, доки не отримаємо останній маршрут. Таким чином, у пам'яті зберігається тільки останній знайдений маршрут, а не всі знайдені, що дає суттєву економію пам'яті. Для реалізації цієї стратегії з'ясуємо, як отримати перший за лексикографічним порядком маршрут, як за знайденим маршрутом знайти наступний і чи існує наступний маршрут для заданого. Для знаходження першого за лексикографічним порядком маршруту довжиною s скористаємось такою його властивістю. Якщо маршрут довжиною s є першим у лексикографічному порядку, то для будь-якого 0<i<s перші i ребер утворюють маршрут, який також буде першим серед усіх маршрутів цієї довжини. Розглянемо на прикладі пошук першого маршруту. Початкова вершина 4. Найменший номер суміжної з нею вершини дорівнює 1. Найменший номер вершини, суміжної з першою, дорівнює 2. Найменший номер вершини, суміжної з другою, дорівнює 1. Отже, перший маршрут за лексикографічним порядком становить 4-1-2-1. Запам’ятаємо його у лінійній таблиці. Отримаємо задачу знаходження наступного за лексикографічним порядком маршруту. Для знаходження наступного маршруту спробуємо збільшити номер останньої вершини. 4-1-2-2 не є маршрутом, тому що у заданому графі вершина 2 не суміжна з собою. 4-1-2-3 є маршрутом. Наступний крок неможливий, тому що остання вершина у шуканому шляху має максимально можливий номер. Це означає, що всі маршрути, що всі маршрути, що починаються на 4-1-2, вже розглянуто. Тому переходимо до пошуку другого маршруту довжиною 2. Це буде маршрут 4-1-3. Переходимо знову до маршрутів довжиною 3. Отримаємо 4-1-3-1, потім 4-1-3-2, потім 4-1-3-4 (4-1-3-3 пропускаємо, тому що вершина 3 несуміжна з собою). 4-1-3-5 не є маршрутом, тому що 4 і 5 вершини несуміжні. Знову переходимо до маршрутів довжини 2 і знаходимо наступний - це буде 4-1-4. Переходимо до довжини 3 і знаходимо 4-1-4-1, 4-1-4-3 та 4-1-4-5. знову переходимо до довжини 2. Наступним маршрутом 4-1-5 не є, бо вершини 1 і 5 несуміжні. Отже, потрібно переходити до довжини 1, послідовність 4-2 не є маршрутом, отож, отримуємо 4-3 і знову переходимо до довжини 2. 4-3-1 є маршрутом, переходимо до довжини 3. Маємо 4-3-1-2, 4-3-1-3 та 4-3-1-4. Далі переходимо до 4-3-2, отримаємо маршрути 4-3-2-1, 4-3-2-3, 4-3-2-5, потім переходимо до 4-3-4, отримуємо 4-3-4-1, 4-3-4-3, 4-3-4-5. Тобто 4-3-4 розглянуто повністю, 4-3-5 – не маршрут, тому 4-3 розглянуто повністю, 4-4 – не маршрут, розглядаємо 4-5. Коли 4-5 буде розглянуто повністю, всі маршрути перераховано. |
