|
В данной статье рассматривается структура данных "система непересекающихся множеств" (на английском "disjoint-set-union", или просто "DSU").
Эта структура данных предоставляет следующие возможности. Изначально имеется несколько элементов, каждый из которых находится в отдельном (своём собственном) множестве. За одну операцию можно объединить два каких-либо множества, а также можно запросить, в каком множестве сейчас находится указанный элемент. Также, в классическом варианте, вводится ещё одна операция — создание нового элемента, который помещается в отдельное множество.
Таким образом, базовый интерфейс данной структуры данных состоит всего из трёх операций:
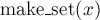 — добавляет новый элемент — добавляет новый элемент  , помещая его в новое множество, состоящее из одного него. , помещая его в новое множество, состоящее из одного него.
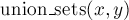 — объединяет два указанных множества (множество, в котором находится элемент — объединяет два указанных множества (множество, в котором находится элемент  , и множество, в котором находится элемент , и множество, в котором находится элемент  ). ).
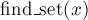 — возвращает, в каком множестве находится указанный элемент — возвращает, в каком множестве находится указанный элемент  . На самом деле при этом возвращается один из элементов множества (называемыйпредставителем или лидером (в англоязычной литературе "leader")). Этот представитель выбирается в каждом множестве самой структурой данных (и может меняться с течением времени, а именно, после вызовов . На самом деле при этом возвращается один из элементов множества (называемыйпредставителем или лидером (в англоязычной литературе "leader")). Этот представитель выбирается в каждом множестве самой структурой данных (и может меняться с течением времени, а именно, после вызовов 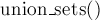 ). ).
Например, если вызов 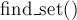 для каких-то двух элементов вернул одно и то же значение, то это означает, что эти элементы находятся в одном и том же множестве, а в противном случае — в разных множествах. для каких-то двух элементов вернул одно и то же значение, то это означает, что эти элементы находятся в одном и том же множестве, а в противном случае — в разных множествах.
Описываемая ниже структура данных позволяет делать каждую из этих операций почти за  в среднем (более подробно об асимптотике см. ниже после описания алгоритма). в среднем (более подробно об асимптотике см. ниже после описания алгоритма).
Также в одном из подразделов статьи описан альтернативный вариант реализации DSU, позволяющий добиться асимптотики 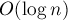 в среднем на один запрос при в среднем на один запрос при 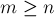 ; а при ; а при 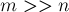 (т.е. (т.е.  значительно больше значительно больше  ) — и вовсе времени ) — и вовсе времени  в среднем на запрос (см. "Хранение DSU в виде явного списка множеств"). в среднем на запрос (см. "Хранение DSU в виде явного списка множеств").
Определимся сначала, в каком виде мы будем хранить всю информацию.
Множества элементов мы будем хранить в виде деревьев: одно дерево соответствует одному множеству. Корень дерева — это представитель (лидер) множества.
При реализации это означает, что мы заводим массив 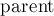 , в котором для каждого элемента мы храним ссылку на его предка в дерева. Для корней деревьев будем считать, что их предок — они сами (т.е. ссылка зацикливается в этом месте). , в котором для каждого элемента мы храним ссылку на его предка в дерева. Для корней деревьев будем считать, что их предок — они сами (т.е. ссылка зацикливается в этом месте).
Мы уже можем написать первую реализацию системы непересекающихся множеств. Она будет довольно неэффективной, но затем мы улучшим её с помощью двух приёмов, получив в итоге почти константное время работы.
Итак, вся информация о множествах элементов хранится у нас с помощью массива 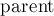 . .
Чтобы создать новый элемент (операция 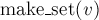 ), мы просто создаём дерево с корнем в вершине ), мы просто создаём дерево с корнем в вершине  , отмечая, что её предок — это она сама. , отмечая, что её предок — это она сама.
Чтобы объединить два множества (операция 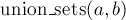 ), мы сначала найдём лидеров множества, в котором находится ), мы сначала найдём лидеров множества, в котором находится  , и множества, в котором находится , и множества, в котором находится  . Если лидеры совпали, то ничего не делаем — это значит, что множества и так уже были объединены. В противном случае можно просто указать, что предок вершины . Если лидеры совпали, то ничего не делаем — это значит, что множества и так уже были объединены. В противном случае можно просто указать, что предок вершины  равен равен  (или наоборот) — тем самым присоединив одно дерево к другому. (или наоборот) — тем самым присоединив одно дерево к другому.
Наконец, реализация операции поиска лидера (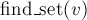 ) проста: мы поднимаемся по предкам от вершины ) проста: мы поднимаемся по предкам от вершины  , пока не дойдём до корня, т.е. пока ссылка на предка не ведёт в себя. Эту операцию удобнее реализовать рекурсивно (особенно это будет удобно позже, в связи с добавляемыми оптимизациями). , пока не дойдём до корня, т.е. пока ссылка на предка не ведёт в себя. Эту операцию удобнее реализовать рекурсивно (особенно это будет удобно позже, в связи с добавляемыми оптимизациями).
void make_set (int v) {
parent[v] = v;
}
int find_set (int v) {
if (v == parent[v])
return v;
return find_set (parent[v]);
}
void union_sets (int a, int b) {
a = find_set (a);
b = find_set (b);
if (a != b)
parent[b] = a;
}
Впрочем, такая реализация системы непересекающихся множеств весьма неэффективна. Легко построить пример, когда после нескольких объединений множеств получится ситуация, что множество — это дерево, выродившееся в длинную цепочку. В результате каждый вызов 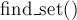 будет работать на таком тесте за время порядка глубины дерева, т.е. за будет работать на таком тесте за время порядка глубины дерева, т.е. за  . .
Это весьма далеко от той асимптотики, которую мы собирались получить (константное время работы). Поэтому рассмотрим две оптимизации, которые позволят (даже применённые по отдельности) значительно ускорить работу.
Эта эвристика предназначена для ускорения работы 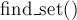 . .
Она заключается в том, что когда после вызова 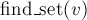 мы найдём искомого лидера мы найдём искомого лидера  множества, то запомним, что у вершины множества, то запомним, что у вершины  и всех пройденных по пути вершин — именно этот лидер и всех пройденных по пути вершин — именно этот лидер  . Проще всего это сделать, перенаправив их . Проще всего это сделать, перенаправив их ![{\rm parent}[]](http://e-maxx.ru/tex2png/cache/21f4cb56d8989f2b1c2ec5bce1983210.png) на эту вершину на эту вершину  . .
Таким образом, у массива предков ![{\rm parent}[]](http://e-maxx.ru/tex2png/cache/21f4cb56d8989f2b1c2ec5bce1983210.png) смысл несколько меняется: теперь это сжатый массив предков, т.е. для каждой вершины там может храниться не непосредственный предок, а предок предка, предок предка предка, и т.д. смысл несколько меняется: теперь это сжатый массив предков, т.е. для каждой вершины там может храниться не непосредственный предок, а предок предка, предок предка предка, и т.д.
С другой стороны, понятно, что нельзя сделать, чтобы эти указатели 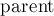 всегда указывали на лидера: иначе при выполнении операции всегда указывали на лидера: иначе при выполнении операции 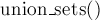 пришлось бы обновлять лидеров у пришлось бы обновлять лидеров у  элементов. элементов.
Таким образом, к массиву ![{\rm parent}[]](http://e-maxx.ru/tex2png/cache/21f4cb56d8989f2b1c2ec5bce1983210.png) следует подходить именно как к массиву предков, возможно, частично сжатому. следует подходить именно как к массиву предков, возможно, частично сжатому.
Новая реализация операции 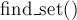 выглядит следующим образом: выглядит следующим образом:
int find_set (int v) {
if (v == parent[v])
return v;
return parent[v] = find_set (parent[v]);
}
Такая простая реализация делает всё, что задумывалось: сначала путём рекурсивных вызовов находится лидера множества, а затем, в процессе раскрутки стека, этот лидер присваивается ссылкам 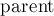 для всех пройденных элементов. для всех пройденных элементов.
Реализовать эту операцию можно и нерекурсивно, но тогда придётся осуществлять два прохода по дереву: первый найдёт искомого лидера, второй — проставит его всем вершинам пути. Впрочем, на практике нерекурсивная реализация не даёт существенного выигрыша.
Покажем, что применение одной эвристики сжатия пути позволяет достичь логарифмическую асимптотику: 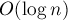 на один запрос в среднем. на один запрос в среднем.
Заметим, что, поскольку операция 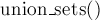 представляет из себя два вызова операции представляет из себя два вызова операции 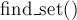 и ещё и ещё  операций, то мы можем сосредоточиться в доказательстве только на оценку времени работы операций, то мы можем сосредоточиться в доказательстве только на оценку времени работы 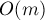 операций операций 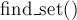 . .
Назовём весом ![w[v]](http://e-maxx.ru/tex2png/cache/037a5a80c288b70567ab5a71619b41e3.png) вершины вершины  число потомков этой вершины (включая её саму). Веса вершин, очевидно, могут только увеличиваться в процессе работы алгоритма. число потомков этой вершины (включая её саму). Веса вершин, очевидно, могут только увеличиваться в процессе работы алгоритма.
Назовём размахом ребра 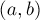 разность весов концов этого ребра: разность весов концов этого ребра: ![|w[a] - w[b]|](http://e-maxx.ru/tex2png/cache/535462d50ca6cb481cab97fed13c7a2b.png) (очевидно, у вершины-предка вес всегда больше, чем у вершины-потомка). Можно заметить, что размах какого-либо фиксированного ребра (очевидно, у вершины-предка вес всегда больше, чем у вершины-потомка). Можно заметить, что размах какого-либо фиксированного ребра 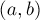 может только увеличиваться в процессе работы алгоритма. может только увеличиваться в процессе работы алгоритма.
Кроме того, разобьём рёбра на классы: будем говорить, что ребро имеет класс  , если его размах принадлежит отрезку , если его размах принадлежит отрезку ![[2^k; 2^{k+1}-1]](http://e-maxx.ru/tex2png/cache/d81fb201323af43e8664bcdbb5c6ba36.png) . Таким образом, класс ребра — это число от . Таким образом, класс ребра — это число от 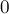 до до 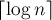 . .
Зафиксируем теперь произвольную вершину  и будем следить, как меняется ребро в её предка: сначала оно отсутствует (пока вершина и будем следить, как меняется ребро в её предка: сначала оно отсутствует (пока вершина  является лидером), затем проводится ребро из является лидером), затем проводится ребро из  в какую-то вершину (когда множество с вершиной в какую-то вершину (когда множество с вершиной  присоединяется к другому множеству), и затем может меняться при сжатии путей в процессе вызовов присоединяется к другому множеству), и затем может меняться при сжатии путей в процессе вызовов 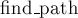 . Понятно, что нас интересует асимптотика только последнего случая (при сжатии путей): все остальные случаи требуют . Понятно, что нас интересует асимптотика только последнего случая (при сжатии путей): все остальные случаи требуют  времени на один запрос. времени на один запрос.
Рассмотрим работу некоторого вызова операции 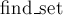 : он проходит в дереве вдоль некоторого пути, стирая все рёбра этого пути и перенаправляя их в лидера. : он проходит в дереве вдоль некоторого пути, стирая все рёбра этого пути и перенаправляя их в лидера.
Рассмотрим этот путь и исключим из рассмотрения последнее ребро каждого класса (т.е. не более чем по одному ребру из класса 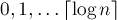 ). Тем самым мы исключили ). Тем самым мы исключили 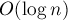 рёбер из каждого запроса. рёбер из каждого запроса.
Рассмотрим теперь все остальные рёбра этого пути. Для каждого такого ребра, если оно имеет класс  , получается, что в этом пути есть ещё одно ребро класса , получается, что в этом пути есть ещё одно ребро класса  (иначе мы были бы обязаны исключить текущее ребро, как единственного представителя класса (иначе мы были бы обязаны исключить текущее ребро, как единственного представителя класса  ). Таким образом, после сжатия пути это ребро заменится на ребро класса как минимум ). Таким образом, после сжатия пути это ребро заменится на ребро класса как минимум 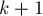 . Учитывая, что уменьшаться вес ребра не может, мы получаем, что для каждой вершины, затронутой запросом . Учитывая, что уменьшаться вес ребра не может, мы получаем, что для каждой вершины, затронутой запросом 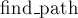 , ребро в её предка либо было исключено, либо строго увеличило свой класс. , ребро в её предка либо было исключено, либо строго увеличило свой класс.
Отсюда мы окончательно получаем асимптотику работы  запросов: запросов: 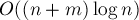 , что (при , что (при 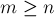 ) означает логарифмическое время работы на один запрос в среднем. ) означает логарифмическое время работы на один запрос в среднем.
Рассмотрим здесь другую эвристику, которая сама по себе способна ускорить время работы алгоритма, а в сочетании с эвристикой сжатия путей и вовсе способна достигнуть практически константного времени работы на один запрос в среднем.
Эта эвристика заключается в небольшом изменении работы 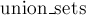 : если в наивной реализации то, какое дерево будет присоединено к какому, определяется случайно, то теперь мы будем это делать на основе рангов. : если в наивной реализации то, какое дерево будет присоединено к какому, определяется случайно, то теперь мы будем это делать на основе рангов.
Есть два варианта ранговой эвристики: в одном варианте рангом дерева называется количество вершин в нём, в другом — глубина дерева (точнее, верхняя граница на глубину дерева, поскольку при совместном применении эвристики сжатия путей реальная глубина дерева может уменьшаться).
В обоих вариантах суть эвристики одна и та же: при выполнении 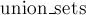 будем присоединять дерево с меньшим рангом к дереву с большим рангом. будем присоединять дерево с меньшим рангом к дереву с большим рангом.
Приведём реализацию ранговой эвристики на основе размеров деревьев:
void make_set (int v) {
parent[v] = v;
size[v] = 1;
}
void union_sets (int a, int b) {
a = find_set (a);
b = find_set (b);
if (a != b) {
if (size[a] < size[b])
swap (a, b);
parent[b] = a;
size[a] += size[b];
}
}
Приведём реализацию ранговой эвристики на основе глубины деревьев:
void make_set (int v) {
parent[v] = v;
rank[v] = 0;
}
void union_sets (int a, int b) {
a = find_set (a);
b = find_set (b);
if (a != b) {
if (rank[a] < rank[b])
swap (a, b);
parent[b] = a;
if (rank[a] == rank[b])
++rank[a];
}
}
Оба варианта ранговой эвристики являются эквивалентными с точки зрения асимптотики, поэтому на практике можно применять любую из них.
Покажем, что асимптотика работы системы непересекающихся множеств при использовании только ранговой эвристики, без эвристики сжатия путей, будет логарифмической на один запрос в среднем: 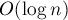 . .
Здесь мы покажем, что при любом из двух вариантов ранговой эвристики глубина каждого дерева будет величиной 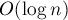 , что автоматически будет означать логарифмическую асимптотику для запроса , что автоматически будет означать логарифмическую асимптотику для запроса 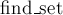 , и, следовательно, запроса , и, следовательно, запроса 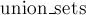 . .
Рассмотрим ранговую эвристику по глубине дерева. Покажем, что если ранг дерева равен  , то это дерево содержит как минимум , то это дерево содержит как минимум 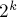 вершин (отсюда будет автоматически следовать, что ранг, а, значит, и глубина дерева, есть величина вершин (отсюда будет автоматически следовать, что ранг, а, значит, и глубина дерева, есть величина 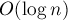 ). Доказывать будем по индукции: для ). Доказывать будем по индукции: для 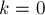 это очевидно. При сжатии путей глубина может только уменьшиться. Ранг дерева увеличивается с это очевидно. При сжатии путей глубина может только уменьшиться. Ранг дерева увеличивается с 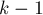 до до  , когда к нему присоединяется дерево ранга , когда к нему присоединяется дерево ранга 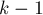 ; применяя к этим двум деревьям размера ; применяя к этим двум деревьям размера 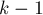 предположение индукции, получаем, что новое дерево ранга предположение индукции, получаем, что новое дерево ранга  действительно будет иметь как минимум действительно будет иметь как минимум 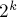 вершин, что и требовалось доказать. вершин, что и требовалось доказать.
Рассмотрим теперь ранговую эвристику по размерам деревьев. Покажем, что если размер дерева равен  , то его высота не более , то его высота не более 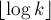 . Доказывать будем по индукции: для . Доказывать будем по индукции: для 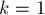 утверждение верно. При сжатии путей глубина может только уменьшиться, поэтому сжатие путей ничего не нарушает. Пусть теперь объединяются два дерева размеров утверждение верно. При сжатии путей глубина может только уменьшиться, поэтому сжатие путей ничего не нарушает. Пусть теперь объединяются два дерева размеров 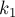 и и 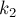 ; тогда по предположению индукции их высоты меньше либо равны, соответственно, ; тогда по предположению индукции их высоты меньше либо равны, соответственно, 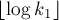 и и 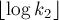 . Не теряя общности, считаем, что первое дерево — большее ( . Не теряя общности, считаем, что первое дерево — большее (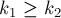 ), поэтому после объединения глубина получившегося дерева из ), поэтому после объединения глубина получившегося дерева из 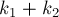 вершин станет равна: вершин станет равна:
![h = \max ( \lfloor \log k_1 \rfloor, 1 + \lfloor [...]](http://e-maxx.ru/tex2png/cache/313f05c20a10998025aecd44f88de465.png)
Чтобы завершить доказательство, надо показать, что:
![h ~ \stackrel{?}{\le} ~ \lfloor \log (k_1+k_2) \r[...]](http://e-maxx.ru/tex2png/cache/c1947a313ad0a57f821bcbbda7c376fe.png)
![2^h = \max ( 2 ^ {\lfloor \log k_1 \rfloor}, 2 ^ [...]](http://e-maxx.ru/tex2png/cache/0fc0ea2e7d0c6a74aaa63dee25719e2d.png)
что есть почти очевидное неравенство, поскольку 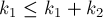 и и 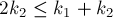 . .
|
