Объединение эвристик: сжатие пути плюс ранговая эвристикаКак уже упоминалось выше, совместное применение этих эвристик даёт особенно наилучший результат, в итоге достигая практически константного времени работы. Мы не будем приводить здесь доказательства асимптотики, поскольку оно весьма объёмно (см., например, Кормен, Лейзерсон, Ривест, Штайн "Алгоритмы. Построение и анализ"). Впервые это доказательство было проведено Тарьяном (1975 г.). Окончательный результат таков: при совместном применении эвристик сжатия пути и объединения по рангу время работы на один запрос получается Именно поэтому про асимптотику работы системы непересекающихся множеств уместно говорить "почти константное время работы". Приведём здесь итоговую реализацию системы непересекающихся множеств, реализующую обе указанные эвристики (используется ранговая эвристика относительно глубин деревьев):
void make_set (int v) { parent[v] = v; rank[v] = 0; } int find_set (int v) { if (v == parent[v]) return v; return parent[v] = find_set (parent[v]); } void union_sets (int a, int b) { a = find_set (a); b = find_set (b); if (a != b) { if (rank[a] < rank[b]) swap (a, b); parent[b] = a; if (rank[a] == rank[b]) ++rank[a]; } }
Применения в задачах и различных улучшенияВ этом разделе мы рассмотрим несколько применений структуры данных "система непересекающихся множеств", как тривиальных, так и использующих некоторые улучшения структуры данных.
Поддержка компонент связности графаЭто одно из очевидных приложений структуры данных "система непересекающихся множеств", которое, по всей видимости, и стимулировало изучение этой структуры. Формально задачу можно сформулировать таким образом: изначально дан пустой граф, постепенно в этот граф могут добавляться вершины и неориентированные рёбра, а также поступают запросы Непосредственно применяя здесь описанную выше структуру данных, мы получаем решение, которое обрабатывает один запрос на добавление вершины/ребра или запрос на проверку двух вершин — за почти константное время в среднем. Учитывая, что практически в точности такая же задача ставится при использовании алгоритма Крускала нахождения минимального остовного дерева, мы сразу же получаемулучшенную версию этого алгоритма, работающую практически за линейное время. Иногда на практике встречается инвертированная версия этой задачи: изначально есть граф с какими-то вершинами и рёбрами, и поступают запросы на удаление рёбер. Если задача дана в оффлайн, т.е. мы заранее можем узнать все запросы, то решать эту задачу можно следующим образом: перевернём задачу задом наперёд: будем считать, что у нас есть пустой граф, в который могут добавляться рёбра (сначала добавим ребро последнего запроса, затем предпоследнего, и т.д.). Тем самым в результате инвертирования этой задачи мы пришли к обычной задаче, решение которой описывалось выше.
Поиск компонент связности на изображенииОдно из лежащих на поверхности применений DSU заключается в решении следующей задачи: имеется изображение Для решения мы просто перебираем все белые клетки изображения, для каждой клетки перебираем её четырёх соседей, и если сосед тоже белый — то вызываем Данную задачу можно решить проще с использованием обхода в глубину (или обхода в ширину), однако у описанного здесь метода есть определённое преимущество: оно может обрабатывать матрицу построчно (оперируя только с текущей строкой, предыдущей строкой и системой непересекающихся множеств, построенной для элементов одной строки), т.е. используя порядка
Поддержка дополнительной информации для каждого множества"Система непересекающихся множеств" позволяет легко хранить любую дополнительную информацию, относящуюся ко множествам. Простой пример — это размеры множеств: как их хранить, было описано при описании ранговой эвристики (информация там записывалась для текущего лидера множества). Таким образом, вместе с лидером каждого множества можно хранить любую дополнительную требуемую в конкретной задаче информацию.
Применение DSU для сжатия "прыжков" по отрезку. Задача о покраске подотрезков в оффлайнеОдно из распространённых применений DSU заключается в том, что если есть набор элементов, и из каждого элемента выходит по одному ребру, то мы можем быстро (за почти константное время) находить конечную точку, в которую мы попадём, если будем двигаться вдоль рёбер из заданной начальной точки. Наглядным примером этого применения является задача о покраске подотрезков: есть отрезок длины Для решения мы можем завести DSU-структуру, которая для каждой клетки будет хранить ссылку на ближайшую справа непокрашенную клетку. Таким образом, изначально каждая клетка указывает на саму себя, а после покраски первого подотрезка — клетка перед началом подотрезка будет указывать на клетку после конца подотрезка. Теперь, чтобы решить задачу, мы рассматриваем запросы перекраски в обратном порядке: от последнего к первому. Для выполнения запроса мы просто каждый раз с помощью нашего DSU находим самую левую непокрашенную клетку внутри отрезка, перекрашиваем её, и перебрасываем указатель из неё на следующую справа пустую клетку. Таким образом, мы здесь фактически используем DSU с эвристикой сжатия путей, но без ранговой эвристики (т.к. нам важно, кто станет лидером после объединения). Следовательно, итоговая асимптотика составит Реализация:
void init() { for (int i=0; i<L; ++i) make_set (i); } void process_query (int l, int r, int c) { for (int v=l; ; ) { v = find_set (v); if (v >= r) break; answer[v] = c; parent[v] = v+1; } } Впрочем, можно реализовать это решение с ранговой эвристикой: будем хранить для каждого множества в некотором массиве
Поддержка расстояний до лидераИногда в конкретных приложениях системы непересекающихся множеств всплывает требование поддерживать расстояние до лидера (т.е. длину пути в рёбрах в дереве от текущей вершины до корня дерева). Если бы не было эвристики сжатия путей, то никаких сложностей бы не возникало — расстояние до корня просто равнялось бы числу рекурсивных вызовов, которые сделала функция Однако в результате сжатия путей несколько рёбер пути могли сжаться в одно ребро. Таким образом, вместе с каждой вершиной придётся хранить дополнительную информацию:длину текущего ребра из вершины в предка. При реализации удобно представлять, что массив
void make_set (int v) { parent[v] = make_pair (v, 0); rank[v] = 0; } pair<int,int> find_set (int v) { if (v != parent[v].first) { int len = parent[v].second; parent[v] = find_set (parent[v].first); parent[v].second += len; } return parent[v]; } void union_sets (int a, int b) { a = find_set (a) .first; b = find_set (b) .first; if (a != b) { if (rank[a] < rank[b]) swap (a, b); parent[b] = make_pair (a, 1); if (rank[a] == rank[b]) ++rank[a]; } } |
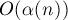 в среднем, где
в среднем, где 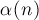 —обратная функция Аккермана, которая растёт очень медленно, настолько медленно, что для всех разумных ограничений
—обратная функция Аккермана, которая растёт очень медленно, настолько медленно, что для всех разумных ограничений  она не превосходит 4 (примерно для
она не превосходит 4 (примерно для 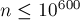 ).
).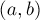 — "в одинаковых ли компонентах связности лежат вершины
— "в одинаковых ли компонентах связности лежат вершины  и
и  ?".
?".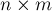 пикселей. Изначально всё изображение белое, но затем на нём рисуется несколько чёрных пикселей. Требуется определить размер каждой "белой" компоненты связности на итоговом изображении.
пикселей. Изначально всё изображение белое, но затем на нём рисуется несколько чёрных пикселей. Требуется определить размер каждой "белой" компоненты связности на итоговом изображении.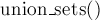 от этих двух вершин. Таким образом, у нас будет DSU с
от этих двух вершин. Таким образом, у нас будет DSU с 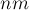 вершинами, соответствующими пикселям изображения. Получившиеся в итоге деревья DSU — и есть искомые компоненты связности.
вершинами, соответствующими пикселям изображения. Получившиеся в итоге деревья DSU — и есть искомые компоненты связности.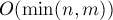 памяти.
памяти.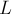 , каждая клетка которого (т.е. каждый кусочек длины
, каждая клетка которого (т.е. каждый кусочек длины  ) имеет нулевой цвет. Поступают запросы вида
) имеет нулевой цвет. Поступают запросы вида 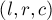 — перекрасить отрезок
— перекрасить отрезок ![[l;r]](http://e-maxx.ru/tex2png/cache/26853b907ea3f6227b00c5afac10292a.png) в цвет
в цвет  . Требуется найти итоговый цвет каждой клетки. Запросы считаются известными заранее, т.е. задача — в оффлайне.
. Требуется найти итоговый цвет каждой клетки. Запросы считаются известными заранее, т.е. задача — в оффлайне.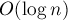 на запрос (впрочем, с маленькой по сравнению с другими структурами данных константой).
на запрос (впрочем, с маленькой по сравнению с другими структурами данных константой).![{\rm end}[]](http://e-maxx.ru/tex2png/cache/a2ca258a437f8aa5be9aac85333e252d.png) , где это множество заканчивается (т.е. самую правую точку). Тогда можно будет объединять два множества в одно по их ранговой эвристике, проставляя потом получившемуся множеству новую правую границу. Тем самым мы получим решение за
, где это множество заканчивается (т.е. самую правую точку). Тогда можно будет объединять два множества в одно по их ранговой эвристике, проставляя потом получившемуся множеству новую правую границу. Тем самым мы получим решение за 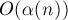 .
.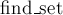 .
.![{\rm parent}[]](http://e-maxx.ru/tex2png/cache/21f4cb56d8989f2b1c2ec5bce1983210.png) и функция
и функция 