|
По аналогии с длиной пути до лидера, так же можно поддерживать чётность длины пути до него. Почему же это применение было выделено в отдельный пункт?
Дело в том, что обычно требование хранение чётности пути всплывает в связи со следующей задачей: изначально дан пустой граф, в него могут добавляться рёбра, а также поступать запросы вида "является ли компонента связности, содержащая данную вершину, двудольной?".
Для решения этой задачи мы можем завести систему непересекающихся множеств для хранения компонент связности, и хранить у каждой вершины чётность длины пути до её лидера. Тем самым, мы можем быстро проверять, приведёт ли добавление указанного ребра к нарушению двудольности графа или нет: а именно, если концы ребра лежат в одной и той же компоненте связности, и при этом имеют одинаковые чётности длины пути до лидера, то добавление этого ребра приведёт к образованию цикла нечётной длины и превращению текущей компоненты в недвудольную.
Главная сложность, с которой мы сталкиваемся при этом, — это то, что мы должны аккуратно, с учётом чётностей, производить объединение двух деревьев в функции 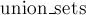 . .
Если мы добавляем ребро 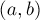 , связывающее две компоненты связности в одну, то при присоединении одного дерева к другому мы должны указать ему такую чётность, чтобы в результате у вершин , связывающее две компоненты связности в одну, то при присоединении одного дерева к другому мы должны указать ему такую чётность, чтобы в результате у вершин  и и  получались бы разные чётности длины пути. получались бы разные чётности длины пути.
Выведём формулу, по которой должна получаться эта чётность, выставляемая лидеру одного множества при присоединении его к лидеру другого множества. Обозначим через  чётность длины пути от вершины чётность длины пути от вершины  до лидера её множества, через до лидера её множества, через  — чётность длины пути от вершины — чётность длины пути от вершины  до лидера её множества, а через до лидера её множества, а через 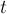 — искомую чётность, которую мы должны поставить присоединяемому лидеру. Если множество с вершиной — искомую чётность, которую мы должны поставить присоединяемому лидеру. Если множество с вершиной  присоединяется к множеству с вершиной присоединяется к множеству с вершиной  , становясь поддеревом, то после присоединения у вершины , становясь поддеревом, то после присоединения у вершины  её чётность не изменится и останется равной её чётность не изменится и останется равной  , а у вершины , а у вершины  чётность станет равной чётность станет равной 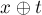 (символом (символом 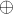 здесь обозначена операция XOR (симметрическая разность)). Нам требуется, чтобы эти две чётности различались, т.е. их XOR был равен единице. Т.е. получаем уравнение на здесь обозначена операция XOR (симметрическая разность)). Нам требуется, чтобы эти две чётности различались, т.е. их XOR был равен единице. Т.е. получаем уравнение на 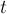 : :
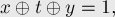
решая которое, находим:
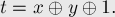
Таким образом, независимо от того, какое множество присоединяется к какому, надо использовать указанную формулу для задания чётности ребра, проводимого из одного лидера к другому.
Приведём реализацию DSU с поддержкой чётностей. Как и в предыдущем пункте, в целях удобства мы используем пары для хранения предков и результата операции 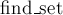 . Кроме того, для каждого множества мы храним в массиве . Кроме того, для каждого множества мы храним в массиве ![{\rm bipartite}[]](http://e-maxx.ru/tex2png/cache/e457bc116fa51d9f5c6a8a4281fc6543.png) , является ли оно всё ещё двудольным или нет. , является ли оно всё ещё двудольным или нет.
void make_set (int v) {
parent[v] = make_pair (v, 0);
rank[v] = 0;
bipartite[v] = true;
}
pair<int,int> find_set (int v) {
if (v != parent[v].first) {
int parity = parent[v].second;
parent[v] = find_set (parent[v].first);
parent[v].second ^= parity;
}
return parent[v];
}
void add_edge (int a, int b) {
pair<int,int> pa = find_set (a);
a = pa.first;
int x = pa.second;
pair<int,int> pb = find_set (b);
b = pb.first;
int y = pb.second;
if (a == b) {
if (x == y)
bipartite[a] = false;
}
else {
if (rank[a] < rank[b])
swap (a, b);
parent[b] = make_pair (a, x ^ y ^ 1);
bipartite[a] &= bipartite[b];
if (rank[a] == rank[b])
++rank[a];
}
}
bool is_bipartite (int v) {
return bipartite[ find_set(v) .first ];
}
Формально задача ставится следующим образом: нужно реализовать структуру данных, которая поддерживает два вида запросов: добавление указанного числа 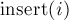 ( ( ) и поиск и извлечение текущего минимального числа ) и поиск и извлечение текущего минимального числа 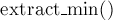 . Будем считать, что каждое число добавляется ровно один раз. . Будем считать, что каждое число добавляется ровно один раз.
Кроме того, считаем, что вся последовательность запросов известна нам заранее, т.е. задача — в оффлайне.
Идея решения следующая. Вместо того, чтобы по очереди отвечать на каждый запрос, переберём число 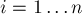 , и определим, ответом на какой запрос это число должно быть. Для этого нам надо найти первый неотвеченный запрос, идущий после добавления , и определим, ответом на какой запрос это число должно быть. Для этого нам надо найти первый неотвеченный запрос, идущий после добавления 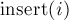 этого числа — легко понять, что это и есть тот запрос, ответом на который является число этого числа — легко понять, что это и есть тот запрос, ответом на который является число  . .
Таким образом, здесь получается идея, похожая на задачу о покраске отрезков.
Можно получить решение за 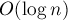 в среднем на запрос, если мы откажемся от ранговой эвристики и будем просто хранить в каждом элементе ссылку на ближайший справа запрос в среднем на запрос, если мы откажемся от ранговой эвристики и будем просто хранить в каждом элементе ссылку на ближайший справа запрос 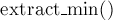 , и использовать сжатие пути для поддержания этих ссылок после объединений. , и использовать сжатие пути для поддержания этих ссылок после объединений.
Также можно получить решение и за 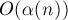 , если мы будем использовать ранговую эвристику и будем хранить в каждом множестве номер позиции, где оно заканчивается (то, что в предыдущем варианте решения достигалось автоматически за счёт того, что ссылки всегда шли только вправо, — теперь надо будет хранить явно). , если мы будем использовать ранговую эвристику и будем хранить в каждом множестве номер позиции, где оно заканчивается (то, что в предыдущем варианте решения достигалось автоматически за счёт того, что ссылки всегда шли только вправо, — теперь надо будет хранить явно).
Алгоритм Тарьяна нахождения LCA за  в среднем в режиме онлайн описан в соответствующей статье. Этот алгоритм выгодно отличается от других алгоритмов поиска LCA своей простотой (особенно по сравнению с оптимальным алгоритмом Фарах-Колтона-Бендера). в среднем в режиме онлайн описан в соответствующей статье. Этот алгоритм выгодно отличается от других алгоритмов поиска LCA своей простотой (особенно по сравнению с оптимальным алгоритмом Фарах-Колтона-Бендера).
Одним из альтернативных способов хранения DSU является сохранение каждого множества в виде явно хранящегося списка его элементов. При этом, у каждого элемента также сохраняется ссылка на представителя (лидера) его множества.
На первый взгляд кажется, что это неэффективная структура данных: при объединении двух множеств мы должны будем добавить один список в конец другого, а также обновить лидера у всех элементов одного из двух списков.
Однако, как оказывается, применение весовой эвристики, аналогичной описанной выше, позволяет существенно снизить асимптотику работы: до 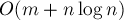 для выполнения для выполнения  запросов над запросов над  элементами. элементами.
Под весовой эвристикой подразумевается, что мы всегда будем добавлять меньшее из двух множеств в большее. Добавление  одного множества в другое легко реализовать за время порядка размера добавляемого множества, а поиск лидера одного множества в другое легко реализовать за время порядка размера добавляемого множества, а поиск лидера  — за время — за время  при таком способе хранения. при таком способе хранения.
Докажем асимптотику 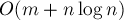 для выполнения для выполнения  запросов. Зафиксируем произвольный элемент запросов. Зафиксируем произвольный элемент  и проследим, как на него воздействовали операции объединения и проследим, как на него воздействовали операции объединения  . Когда на элемент . Когда на элемент  воздействовали первый раз, мы можем утверждать, что размер его нового множества будет как минимум воздействовали первый раз, мы можем утверждать, что размер его нового множества будет как минимум  . Когда на . Когда на  воздействовали второй раз — можно утверждать, что он попадёт в множество размера не менее воздействовали второй раз — можно утверждать, что он попадёт в множество размера не менее  (т.к. мы добавляем меньшее множество в большее). И так далее — получаем, что на элемент (т.к. мы добавляем меньшее множество в большее). И так далее — получаем, что на элемент  могло воздействовать максимум могло воздействовать максимум 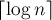 операций объединения. Таким образом, в сумме по всем вершинам это составляет операций объединения. Таким образом, в сумме по всем вершинам это составляет 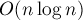 , плюс по , плюс по  на каждый запрос — что и требовалось доказать. на каждый запрос — что и требовалось доказать.
Приведём пример реализации:
vector<int> lst[MAXN];
int parent[MAXN];
void make_set (int v) {
lst[v] = vector<int> (1, v);
parent[v] = v;
}
int find_set (int v) {
return parent[v];
}
void union_sets (int a, int b) {
a = find_set (a);
b = find_set (b);
if (a != b) {
if (lst[a].size() < lst[b].size())
swap (a, b);
while (!lst[b].empty()) {
int v = lst[b].back();
lst[b].pop_back();
parent[v] = a;
lst[a].push_back (v);
}
}
}
Также эту идею добавления элементов меньшего множества в большее можно использовать и вне рамок DSU, при решении других задач.
Например, рассмотрим следующую задачу: дано дерево, каждому листу которого приписано какое-либо число (одно и то же число может встречаться несколько раз у разных листьев). Требуется для каждой вершины дерева узнать количество различных чисел в её поддереве.
Применив в этой задаче эту же идею, можно получить такое решение: пустим обход в глубину по дереву, который будет возвращать указатель на  чисел — список всех чисел в поддереве этой вершины. Тогда, чтобы получить ответ для текущей вершины (если, конечно, она не лист) — надо вызвать обход в глубину от всех детей этой вершины, и объединить все полученные чисел — список всех чисел в поддереве этой вершины. Тогда, чтобы получить ответ для текущей вершины (если, конечно, она не лист) — надо вызвать обход в глубину от всех детей этой вершины, и объединить все полученные  в один, размер которого и будет ответом для текущей вершины. Для эффективного объединения нескольких в один, размер которого и будет ответом для текущей вершины. Для эффективного объединения нескольких 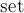 в один как раз применим описанный выше приём: будем объединять два множества, просто добавляя по одному элементы меньшего множества в большее. В итоге мы получим решение за в один как раз применим описанный выше приём: будем объединять два множества, просто добавляя по одному элементы меньшего множества в большее. В итоге мы получим решение за 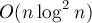 , поскольку добавление одного элемента в , поскольку добавление одного элемента в 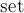 производится за производится за 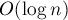 . .
Одно из мощных применений структуры данных "системы непересекающихся множеств" заключается в том, что она позволяет хранить одновременно как сжатую, так и несжатую структуру деревьев. Сжатая структура может использоваться для быстрого объединения деревьев и проверки на принадлежность двух вершин одному дереву, а несжатая — например, для поиска пути между двумя заданными вершинами, или прочих обходов структуры дерева.
При реализации это означает, что помимо обычного для DSU массива сжатых предков ![{\rm parent}[]](http://e-maxx.ru/tex2png/cache/21f4cb56d8989f2b1c2ec5bce1983210.png) мы заведём массив обычных, несжатых, предков мы заведём массив обычных, несжатых, предков ![{\rm real\_parent}[]](http://e-maxx.ru/tex2png/cache/75cee40f8ae8df680b9cbdf86459344a.png) . Понятно, что поддержание такого массива никак не ухудшает асимптотику: изменения в нём происходят только при объединении двух деревьев, и лишь в одном элементе. . Понятно, что поддержание такого массива никак не ухудшает асимптотику: изменения в нём происходят только при объединении двух деревьев, и лишь в одном элементе.
С другой стороны, при применении на практике нередко требуется научиться соединять два дерева указанным ребром, не обязательно выходящим из их корней. Это означает, что у нас нет другого выхода, кроме как переподвесить одно из деревьев за указанную вершину, чтобы затем мы смогли присоединить это дерево к другому, сделав корень этого дерева дочерней вершиной ко второму концу добавляемого ребра.
На первый взгляд кажется, что операция переподвешивания — очень затратна и сильно ухудшит асимптотику. Действительно, для переподвешивания дерева за вершину  мы должны пройтись от этой вершины до корня дерева, обновляя везде указатели мы должны пройтись от этой вершины до корня дерева, обновляя везде указатели ![{\rm parent}[]](http://e-maxx.ru/tex2png/cache/21f4cb56d8989f2b1c2ec5bce1983210.png) и и ![{\rm real\_parent}[]](http://e-maxx.ru/tex2png/cache/75cee40f8ae8df680b9cbdf86459344a.png) . .
Однако на самом деле всё не так плохо: достаточно лишь переподвешивать то из двух деревьев, которое меньше, чтобы получить асимпотику одного объединения, равную 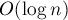 в среднем. в среднем.
Более подробно (включая доказательства асимптотики) см. алгоритм поиска мостов в графе за 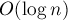 в среднем в онлайне. в среднем в онлайне.
Структура данных "система непересекающихся множеств" была известна сравнительно давно.
Способ хранения этой структуры в виде леса деревьев был, по всей видимости, впервые описан Галлером и Фишером в 1964 г. (Galler, Fisher "An Improved Equivalence Algorithm"), однако полный анализ асимптотики был проведён гораздо позже.
Эвристики сжатия путей и объединения по рангу, по-видимому, разработали МакИлрой (McIlroy) и Моррис (Morris), и, независимо от них, Триттер (Tritter).
Некоторое время была известна лишь оценка 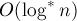 на одну операцию в среднем, данная Хопкрофтом и Ульманом в 1973 г. (Hopcroft, Ullman "Set-merging algomthms") — здесь на одну операцию в среднем, данная Хопкрофтом и Ульманом в 1973 г. (Hopcroft, Ullman "Set-merging algomthms") — здесь 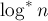 — итерированный логарифм (это медленно растущая функция, но всё же не настолько медленно, как обратная функция Аккермана). — итерированный логарифм (это медленно растущая функция, но всё же не настолько медленно, как обратная функция Аккермана).
Впервые оценку 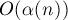 , где , где 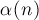 — обратная функция Аккермана — получил Тарьян в своей статье 1975 г. (Tarjan "Efficiency of a Good But Not Linear Set Union Algorithm"). Позже в 1985 г. он вместе с Льювеном получил эту временную оценку для нескольких различных ранговых эвристик и способов сжатия пути (Tarjan, Leeuwen "Worst-Case Analysis of Set Union Algorithms"). — обратная функция Аккермана — получил Тарьян в своей статье 1975 г. (Tarjan "Efficiency of a Good But Not Linear Set Union Algorithm"). Позже в 1985 г. он вместе с Льювеном получил эту временную оценку для нескольких различных ранговых эвристик и способов сжатия пути (Tarjan, Leeuwen "Worst-Case Analysis of Set Union Algorithms").
Наконец, Фредман и Сакс в 1989 г. доказали, что в принятой модели вычислений любой алгоритм для системы непересекающихся множеств должен работать как минимум за 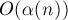 в среднем (Fredman, Saks "The cell probe complexity of dynamic data structures"). в среднем (Fredman, Saks "The cell probe complexity of dynamic data structures").
Впрочем, следует также отметить, что есть несколько статей, оспаривающих эту временную оценку и утверждающих, что система непересекающихся множеств с эвристиками сжатия пути и объединения по рангу работает за  в среднем: Zhang "The Union-Find Problem Is Linear", Wu, Otoo "A Simpler Proof of the Average Case Complexity of Union-Find with Path Compression". в среднем: Zhang "The Union-Find Problem Is Linear", Wu, Otoo "A Simpler Proof of the Average Case Complexity of Union-Find with Path Compression".
|
 .
.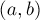 , связывающее две компоненты связности в одну, то при присоединении одного дерева к другому мы должны указать ему такую чётность, чтобы в результате у вершин
, связывающее две компоненты связности в одну, то при присоединении одного дерева к другому мы должны указать ему такую чётность, чтобы в результате у вершин  и
и  получались бы разные чётности длины пути.
получались бы разные чётности длины пути. чётность длины пути от вершины
чётность длины пути от вершины  — чётность длины пути от вершины
— чётность длины пути от вершины 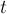 — искомую чётность, которую мы должны поставить присоединяемому лидеру. Если множество с вершиной
— искомую чётность, которую мы должны поставить присоединяемому лидеру. Если множество с вершиной 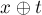 (символом
(символом 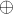 здесь обозначена операция XOR (симметрическая разность)). Нам требуется, чтобы эти две чётности различались, т.е. их XOR был равен единице. Т.е. получаем уравнение на
здесь обозначена операция XOR (симметрическая разность)). Нам требуется, чтобы эти две чётности различались, т.е. их XOR был равен единице. Т.е. получаем уравнение на 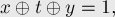
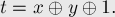
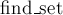 . Кроме того, для каждого множества мы храним в массиве
. Кроме того, для каждого множества мы храним в массиве ![{\rm bipartite}[]](http://e-maxx.ru/tex2png/cache/e457bc116fa51d9f5c6a8a4281fc6543.png) , является ли оно всё ещё двудольным или нет.
, является ли оно всё ещё двудольным или нет.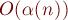 в среднем в оффлайне
в среднем в оффлайне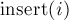 (
(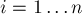 ) и поиск и извлечение текущего минимального числа
) и поиск и извлечение текущего минимального числа 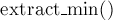 . Будем считать, что каждое число добавляется ровно один раз.
. Будем считать, что каждое число добавляется ровно один раз. .
.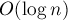 в среднем на запрос, если мы откажемся от ранговой эвристики и будем просто хранить в каждом элементе ссылку на ближайший справа запрос
в среднем на запрос, если мы откажемся от ранговой эвристики и будем просто хранить в каждом элементе ссылку на ближайший справа запрос 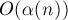 , если мы будем использовать ранговую эвристику и будем хранить в каждом множестве номер позиции, где оно заканчивается (то, что в предыдущем варианте решения достигалось автоматически за счёт того, что ссылки всегда шли только вправо, — теперь надо будет хранить явно).
, если мы будем использовать ранговую эвристику и будем хранить в каждом множестве номер позиции, где оно заканчивается (то, что в предыдущем варианте решения достигалось автоматически за счёт того, что ссылки всегда шли только вправо, — теперь надо будет хранить явно). в среднем в режиме онлайн описан в
в среднем в режиме онлайн описан в 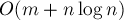 для выполнения
для выполнения  запросов над
запросов над  элементами.
элементами.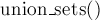 одного множества в другое легко реализовать за время порядка размера добавляемого множества, а поиск лидера
одного множества в другое легко реализовать за время порядка размера добавляемого множества, а поиск лидера  — за время
— за время 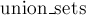 . Когда на элемент
. Когда на элемент 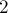 . Когда на
. Когда на 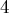 (т.к. мы добавляем меньшее множество в большее). И так далее — получаем, что на элемент
(т.к. мы добавляем меньшее множество в большее). И так далее — получаем, что на элемент 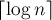 операций объединения. Таким образом, в сумме по всем вершинам это составляет
операций объединения. Таким образом, в сумме по всем вершинам это составляет 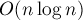 , плюс по
, плюс по 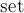 чисел — список всех чисел в поддереве этой вершины. Тогда, чтобы получить ответ для текущей вершины (если, конечно, она не лист) — надо вызвать обход в глубину от всех детей этой вершины, и объединить все полученные
чисел — список всех чисел в поддереве этой вершины. Тогда, чтобы получить ответ для текущей вершины (если, конечно, она не лист) — надо вызвать обход в глубину от всех детей этой вершины, и объединить все полученные 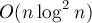 , поскольку добавление одного элемента в
, поскольку добавление одного элемента в 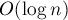 .
.![{\rm parent}[]](http://e-maxx.ru/tex2png/cache/21f4cb56d8989f2b1c2ec5bce1983210.png) мы заведём массив обычных, несжатых, предков
мы заведём массив обычных, несжатых, предков ![{\rm real\_parent}[]](http://e-maxx.ru/tex2png/cache/75cee40f8ae8df680b9cbdf86459344a.png) . Понятно, что поддержание такого массива никак не ухудшает асимптотику: изменения в нём происходят только при объединении двух деревьев, и лишь в одном элементе.
. Понятно, что поддержание такого массива никак не ухудшает асимптотику: изменения в нём происходят только при объединении двух деревьев, и лишь в одном элементе. мы должны пройтись от этой вершины до корня дерева, обновляя везде указатели
мы должны пройтись от этой вершины до корня дерева, обновляя везде указатели 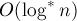 на одну операцию в среднем, данная Хопкрофтом и Ульманом в 1973 г. (Hopcroft, Ullman "Set-merging algomthms") — здесь
на одну операцию в среднем, данная Хопкрофтом и Ульманом в 1973 г. (Hopcroft, Ullman "Set-merging algomthms") — здесь 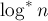 — итерированный логарифм (это медленно растущая функция, но всё же не настолько медленно, как обратная функция Аккермана).
— итерированный логарифм (это медленно растущая функция, но всё же не настолько медленно, как обратная функция Аккермана).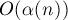 , где
, где 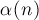 — обратная функция Аккермана — получил Тарьян в своей статье 1975 г. (Tarjan "Efficiency of a Good But Not Linear Set Union Algorithm"). Позже в 1985 г. он вместе с Льювеном получил эту временную оценку для нескольких различных ранговых эвристик и способов сжатия пути (Tarjan, Leeuwen "Worst-Case Analysis of Set Union Algorithms").
— обратная функция Аккермана — получил Тарьян в своей статье 1975 г. (Tarjan "Efficiency of a Good But Not Linear Set Union Algorithm"). Позже в 1985 г. он вместе с Льювеном получил эту временную оценку для нескольких различных ранговых эвристик и способов сжатия пути (Tarjan, Leeuwen "Worst-Case Analysis of Set Union Algorithms").