Sqrt-декомпозицияSqrt-декомпозиция — это метод, или структура данных, которая позволяет выполнять некоторые типичные операции (суммирование элементов подмассива, нахождение минимума/максимума и т.д.) за Сначала мы опишем структуру данных для одного из простейших применений этой идеи, затем покажем, как обобщать её для решения некоторых других задач, и, наконец, рассмотрим несколько иное применение этой идеи: разбиение входных запросов на sqrt-блоки.
Структура данных на основе sqrt-декомпозицииПоставим задачу. Дан массив
ОписаниеОсновная идея sqrt-декомпозиции заключается в том, что сделаем следующий предпосчёт: разделим массив Можно считать, что длина одного блока и количество блоков равны одному и тому же числу — корню из
тогда массив
Хотя последний блок может содержать меньше, чем Таким образом, для каждого блока
Итак, пусть эти значения Иллюстрация (здесь через
На этом рисунке видно, что для того чтобы посчитать сумму в отрезке
(примечание: эта формула неверна, когда Тем самым мы экононим значительное количество операций. Действительно, размер каждого из "хвостов", очевидно, не превосходит длины блока
РеализацияПриведём сначала простейшую реализацию:
// входные данные int n; vector<int> a (n); // предпосчёт int len = (int) sqrt (n + .0) + 1; // и размер блока, и количество блоков vector<int> b (len); for (int i=0; i<n; ++i) b[i / len] += a[i]; // ответ на запросы for (;;) { int l, r; // считываем входные данные - очередной запрос int sum = 0; for (int i=l; i<=r; ) if (i % len == 0 && i + len - 1 <= r) { // если i указывает на начало блока, целиком лежащего в [l;r] sum += b[i / len]; i += len; } else { sum += a[i]; ++i; } } Недостатком этой реализации является то, что в ней неоправданно много операций деления (которые, как известно, выполняются значительно медленнее других операций). Вместо этого можно посчитать номера блоков
int sum = 0; int c_l = l / len, c_r = r / len; if (c_l == c_r) for (int i=l; i<=r; ++i) sum += a[i]; else { for (int i=l, end=(c_l+1)*len-1; i<=end; ++i) sum += a[i]; for (int i=c_l+1; i<=c_r-1; ++i) sum += b[i]; for (int i=c_r*len; i<=r; ++i) sum += a[i]; }
Другие задачиМы рассматривали задачу нахождения суммы элементов массива в каком-то его подотрезке. Эту задачу можно немного расширить: разрешим также меняться отдельным элементам массива
С другой стороны, вместо задачи о сумме аналогично можно решать задачи о минимальном, максимальном элементах в отрезке. Если в этих задачах допускать изменения отдельных элементов, то тоже надо будет пересчитывать значение Аналогичным образом sqrt-декомпозицию можно применять и для множества других подобных задач: нахождение количества нулевых элементов, первого ненулевого элемента, подсчёта количества определённых элементов, и т.д. Есть и целый класс задач, когда происходят изменения элементов на целом подотрезке: прибавление или присвоение элементов на каком-то подотрезке массива Например, нужно выполнять следующие два вида запросов: прибавить ко всем элементам некоторого отрезка Наконец, можно комбинировать оба вида задач: изменение элементов на отрезке и ответ на запросы тоже на отрезке. Оба вида операций будут выполняться за Можно привести пример и других задач, к которым можно применить sqrt-декомпозицию. Например, можно решать задачу о поддержании множества чисел с возможностью добавления/удаления чисел, проверки числа на принадлежность множеству, поиск
Sqrt-декомпозиция входных запросовРассмотрим теперь совершенно иное применение идеи об sqrt-декомпозиции. Предположим, что у нас есть некоторая задача, в которой нам даются некоторые входные данные, а затем поступают Конкретная задача может быть весьма сложной, и "честное" её решение (которое считывает один запрос, обрабатывает его, изменяя состояние системы, и возвращает ответ) может быть технически сложным или вовсе быть не по силам для решающего. С другой стороны, решение "оффлайнового" варианта задачи, т.е. когда отсутствуют модифицирующие операции, а имеются только лишь запрашивающие запросы — часто оказывается гораздо проще. Предположим, что мы умеем решать "оффлайновый" вариант задачи, т.е. строить за некоторое время Тогда разобьём входные запросы на блоки (какой длины — пока не уточняем; обозначим эту длину через Теперь будем по очереди брать запросы из текущего блока и обрабатывать каждый из них. Если текущий запрос — модифицирующий, то пропустим его. Если же текущий запрос — запрашивающий, то обратимся к структуре данных для оффлайнового варианта задачи, но предварительно учтя все модифицирующие запросы в текущем блоке. Такое учитывание модифицирующих запросов бывает возможным далеко не всегда, и оно должно происходить достаточно быстро — за время Таким образом, если всего у нас Поскольку приведённые выше рассуждения слишком абстрактны, приведём несколько примеров задач, к которым применима такая sqrt-декомпозиция.
Пример задачи: прибавление на отрезкеУсловие задачи: дан массив чисел Хотя эту задачу можно решать и без этого приёма с разбиением запросов на блоки, мы приведём её здесь — как простейшее и наглядное применение этого метода. Итак, разобьём входные запросы на блоки по Таким образом, мы научились отвечать на запрашивающие запросы за время Осталось только заметить, что в конце каждого блока запросов мы должны применить все модифицирующие запросы этого блока к массиву Таким образом, итоговая асимптотика решения составит
Пример задачи: disjoint-set-union с разделениемЕсть неориентированный граф с Если бы запросы удаления отсутствовали, то решением задачи была бы известная структура данных disjoint-set-union (система непересекающихся множеств). Однако при наличии удалений задача значительно усложняется. Сделаем следующим образом. В начале каждого блока запросов посмотрим, какие рёбра в этом блоке будут удаляться, и сразу удалим их из графа. Теперь построим систему непересекающихся множеств (dsu) на полученном графе. Как мы теперь должны отвечать на очередной запрос из текущего блока? Наша система непересекающихся множеств "знает" обо всех рёбрах, кроме тех, что добавляются/удаляются в текущем блоке. Однако удаления из dsu нам делать уже не надо — мы заранее удалили все такие рёбра из графа. Таким образом, всё, что может быть — это дополнительные, добавляющиеся рёбра, которых может быть максимум Следовательно, при ответе на текущий запрашивающий запрос мы можем просто пустить обход в ширину по компонентам связности dsu, который отработает за
Оффлайновые задачи на запросы на подотрезках массива и универсальная sqrt-эвристика для нихРассмотрим ещё одну интересную вариацию идеи sqrt-декомпозиции. Пусть у нас есть некоторая задача, в которой есть массив чисел, и поступают запрашивающие запросы, имеющие вид Наконец, введём последнее ограничение: мы считаем, что умеем быстро пересчитывать ответ на запрос при изменении левой или правой границы на единицу. Т.е. если мы знали ответ на запрос
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

|
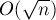 , что значительно быстрее, чем
, что значительно быстрее, чем  для тривиального алгоритма.
для тривиального алгоритма.![a[0 \ldots n-1]](http://e-maxx.ru/tex2png/cache/2f7c3ec9c849a4dcbfc3195989056b93.png) . Требуется реализовать такую структуру данных, которая сможет находить сумму элементов
. Требуется реализовать такую структуру данных, которая сможет находить сумму элементов ![a[l \ldots r]](http://e-maxx.ru/tex2png/cache/61de5ad6b5b41c84e862798a8f59f0a9.png) для произвольных
для произвольных 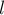 и
и 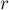 за
за  на блоки длины примерно
на блоки длины примерно 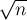 , и в каждом блоке
, и в каждом блоке  заранее предпосчитаем сумму
заранее предпосчитаем сумму ![b[i]](http://e-maxx.ru/tex2png/cache/e875235207203e3980be2bd509460e7a.png) элементов в нём.
элементов в нём. , округлённому вверх:
, округлённому вверх: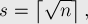
![a[]](http://e-maxx.ru/tex2png/cache/0f0e294f3fa9d716ea988ff8370f698d.png) разбивается на блоки примерно таким образом:
разбивается на блоки примерно таким образом:![\underbrace{ a[0] ~ a[1] ~ \ldots ~ a[s-1] }_{b[0[...]](http://e-maxx.ru/tex2png/cache/662da4cbdb10ce5be7fc046667cde348.png)
 , элементов (если
, элементов (если  мы знаем сумму на нём
мы знаем сумму на нём ![b[k]](http://e-maxx.ru/tex2png/cache/e41b82131f67211d919da00859e908b9.png) :
:![b[k] = \sum_{i=k \cdot s}^{\min (n-1, (k+1) \cdot[...]](http://e-maxx.ru/tex2png/cache/f2fe22971a0f5830959a5164f611dbd9.png)
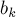 предварительно подсчитаны (для этого надо, очевидно,
предварительно подсчитаны (для этого надо, очевидно, 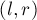 ? Заметим, что если отрезок
? Заметим, что если отрезок ![[l;r]](http://e-maxx.ru/tex2png/cache/26853b907ea3f6227b00c5afac10292a.png) длинный, то в нём будут содержаться несколько блоков целиком, и на такие блоки мы можем узнать сумму на них за одну операцию. В итоге от всего отрезка
длинный, то в нём будут содержаться несколько блоков целиком, и на такие блоки мы можем узнать сумму на них за одну операцию. В итоге от всего отрезка  — номер блока, в котором лежит
— номер блока, в котором лежит ![\ldots ~ \overbrace{ a[l] ~ \ldots ~ a[(k+1) \cdo[...]](http://e-maxx.ru/tex2png/cache/591460c780d6658d53231703eb0ed3ba.png)
![[l \ldots r]](http://e-maxx.ru/tex2png/cache/653023af1da32cf3f51fe321fa0778da.png) , надо просуммировать элементы только в двух "хвостах":
, надо просуммировать элементы только в двух "хвостах": ![[l \ldots (k+1) \cdot s-1]](http://e-maxx.ru/tex2png/cache/31a3de8a513ac2a8ce7cd9e031bc17c1.png) и
и ![[p \cdot s \ldots r]](http://e-maxx.ru/tex2png/cache/c9aef1a7216556e01c0d969353aad25e.png) , и просуммировать значения
, и просуммировать значения 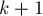 и заканчивая
и заканчивая 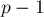 :
:![\sum_{i=l}^{r} a[i] = \sum_{i=l}^{(k+1) \cdot s-1[...]](http://e-maxx.ru/tex2png/cache/cdba4a8584445ee8e23b643b55564844.png)
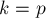 : в таком случае некоторые элементы будут просуммированы дважды; в этом случае надо просто просуммировать элементы с
: в таком случае некоторые элементы будут просуммированы дважды; в этом случае надо просто просуммировать элементы с 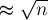 , то всего для вычисления суммы на отрезке
, то всего для вычисления суммы на отрезке 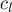 и
и 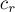 , в которых лежат границы
, в которых лежат границы 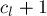 по
по 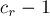 , отдельно обработав "хвосты" в блоках
, отдельно обработав "хвосты" в блоках 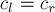 становится особым и требует отдельной обработки:
становится особым и требует отдельной обработки: . Действительно, если меняется какой-то элемент
. Действительно, если меняется какой-то элемент 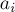 , то достаточно обновить значение
, то достаточно обновить значение 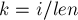 ):
):![b[k] += a[i] - old\_a[i].](http://e-maxx.ru/tex2png/cache/69c2bbc50be3a3a96149c9725fe5f2c5.png)
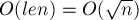 операций.
операций.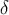 , и узнавать значение отдельного элемента
, и узнавать значение отдельного элемента 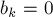 ); тогда при выполнении запроса "прибавление" нужно будет выполнить прибавление ко всем элементам
); тогда при выполнении запроса "прибавление" нужно будет выполнить прибавление ко всем элементам 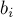 для блоков, целиком лежащих в отрезке
для блоков, целиком лежащих в отрезке 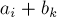 , где
, где  .
. и
и  : один — для обеспечения изменений на отрезке, другой — для ответа на запросы.
: один — для обеспечения изменений на отрезке, другой — для ответа на запросы.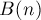 некую структуру данных, которая может отвечать на запросы, но не умеет обрабатывать модифицирующие запросы.
некую структуру данных, которая может отвечать на запросы, но не умеет обрабатывать модифицирующие запросы.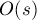 или немного хуже; обозначим это время через
или немного хуже; обозначим это время через 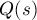 .
. запросов, то на их обработку потребуется
запросов, то на их обработку потребуется 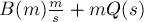 времени. Величину
времени. Величину 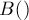 и
и 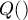 . Например, если
. Например, если 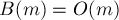 и
и 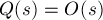 , то оптимальным выбором будет
, то оптимальным выбором будет 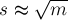 , и итоговая асимптотика получится
, и итоговая асимптотика получится 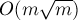 .
.![a[1 \ldots n]](http://e-maxx.ru/tex2png/cache/882c9eac4789d4397cc304ec6933ec6e.png) , и поступают запросы двух видов: узнать значение в
, и поступают запросы двух видов: узнать значение в  ко всем элементам массива в некотором отрезке
ко всем элементам массива в некотором отрезке ![a[l \dots r]](http://e-maxx.ru/tex2png/cache/301805acd8bb348b42f7e89540ac8d84.png) .
.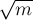 (где
(где ![a[i]](http://e-maxx.ru/tex2png/cache/3530c8c1281c8ee618b020a2333a22ca.png) . Затем пройдёмся по всем пропущенным в этом блоке запросам прибавления, и для тех из них, в которые попадает
. Затем пройдёмся по всем пропущенным в этом блоке запросам прибавления, и для тех из них, в которые попадает 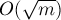 .
.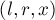 отметить в вспомогательном массиве в точке
отметить в вспомогательном массиве в точке 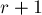 — число
— число 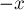 , и затем пройтись по этому массиву, прибавляя текущую сумму к массиву
, и затем пройтись по этому массиву, прибавляя текущую сумму к массиву 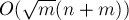 .
.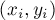 , удалить ребро
, удалить ребро 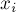 и
и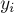 путём.
путём.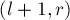 или
или 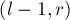 или
или