|
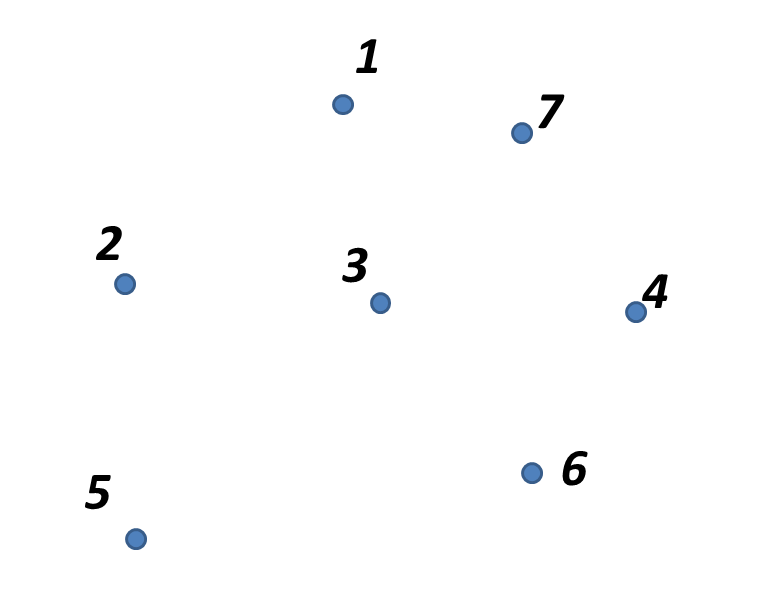
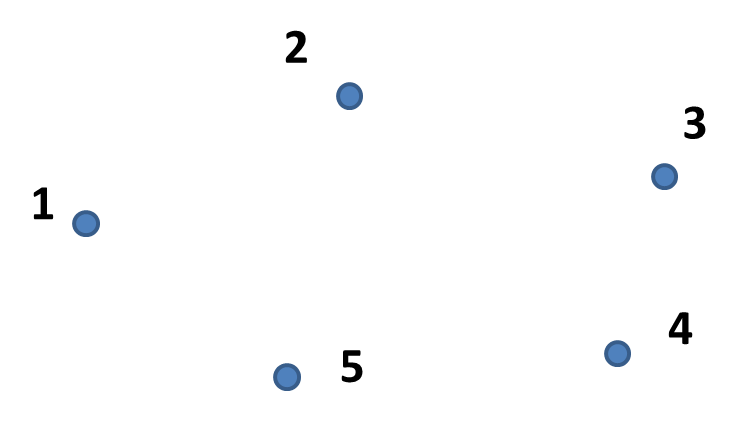
Введення в теорію графів Розглянемо будь-яку скінчену множину елементів (міста на карті, комп’ютери в мережі, люди в соціальних мережах і т.д.) та покажемо їх точками на площині з довільним розташуванням. Цю множину будемо називати множиною вершин графа V (від англ. vertex – вершина). Вершини графа зручно позначати цифрами V={1, 2, …, n} або буквами V={a, b, c, …} (мал.1).
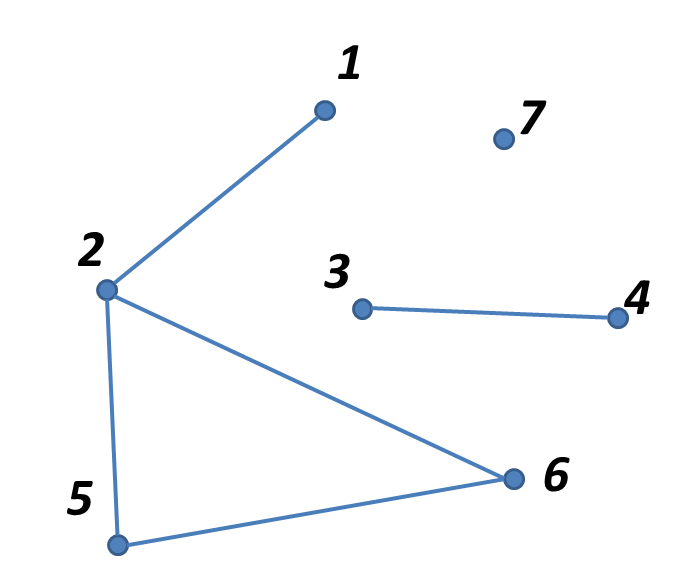
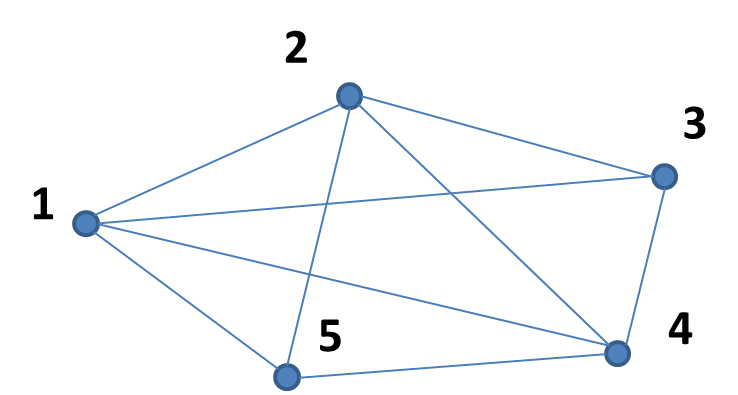
Мал.1 Множина вершин. Зв’язки між елементами множини покажемо у вигляді ліній, які з’єднують відповідні точки – ребер. Множина ребер графа задається множиною пар вершин E (від англ. edge – ребро)(мал.2).
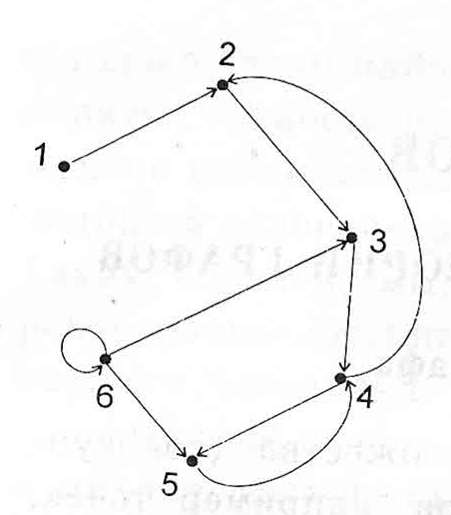
Мал.2 Множина ребер. Граф – це множина вершин V та множина ребер E. Приклад. V={1, 2, 3, 4, 5}, E={(1,2), (2,3), (3,4), (2,4)}. Якщо зв’язок між елементами множини односторонній, то його зображають у вигляді лінії із стрілкою – дугою. Граф в цьому випадку називають орієнтованим або орграфом (мал.3). Дуга – це пара вершин графа, одна з яких є початком, а інша кінцем дуги. Приклад. V={1, 2, 3, 4, 5, 6}, E={(1, 2), (2, 3), (3,4), (4,5), (4,2), (5,4), (6,5), (6,3), (6,6)}. Ребро, яке з’єднує вершину з собою називається петлею.
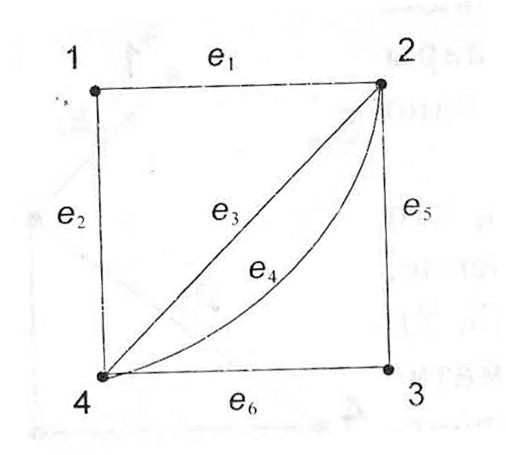
Мал. 3 Орграф. Якщо між двома вершинами є можливість декількох ребер, то такий граф називають мультиграфом або кратним графом. Ребра, які з’єднують однакові вершини називають паралельними або кратними ребрами (мал.4).
Мал. 4 Мультиграф. Граф називають порожнім графом, якщо в ньому немає ребер (мал.5).
Мал. 5. Порожній граф. Повним графом називають граф, в якому будь-яка пара вершин з’єднана ребром (мал. 6).
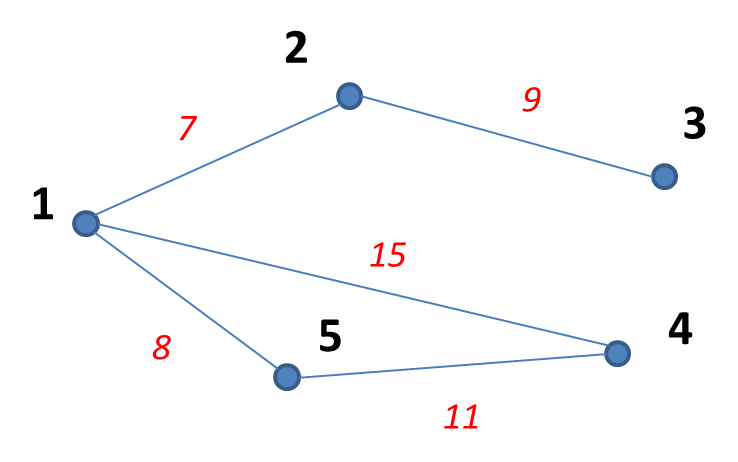
Мал. 6. Повний граф. Навантаженим графом або сіткою називають граф, в якому кожному ребру відповідає число (вага ребра) (мал. 8). Мал. 7. Навантажений граф або сітка. Джерела: disted.edu.vn.ua |