|
Зв'язність графа. Впродовж даного уроку розглядатимемо лише неорієнтовані та ненавантажені графи. Означення. Граф називається зв'язним, якщо існує хоча б один маршрут між будь-якими двома його вершинами. Вважаємо, що маршрут, що веде від деякої вершини в ту саму вершину, завжди існує, навіть коли ця вершина ізольована (в такому випадку маршрут не містить жодного ребра). Тому граф, що містить єдину вершину, зв'язний. Граф, у якому більше одної вершини і який має хоча б одну ізольовану вершину, не є зв'язним. Означення. Дві вершини, між якими існує хоча б один маршрут, називаються досяжними. Властивості досяжності. 1. Кожна вершина графа досяжна з самої себе. 2. Якщо вершина a досяжна з вершини b, то вершина b досяжна з вершини a. 3. Якщо вершина a досяжна з вершини b і вершина b досяжна з вершини c, то вершина a досяжна з вершини c. Приклади.
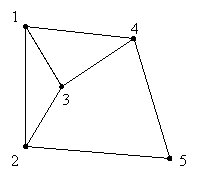
Малюнок 1
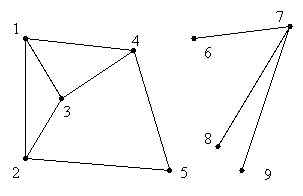
Малюнок 2 Граф, зображений на малюнку 1, зв'язний, а на малюнку 2 - не є, тому що не існує шляху, наприклад, з вершини 1 до вершини 7. Як перевірити, чи є заданий граф зв'язним? Якщо скористатись означенням, необхідно перевірити всі пари вершин, чи є шлях між ними. Але виявляється, що можна перевіряти не всі пари. Справедливе таке твердження. Граф зв'язний тоді і тільки тоді, коли існують шляхи від довільної вершини до всіх інших. Доведемо це твердження. Виберемо вершину k. Дійсно, якщо граф є зв'язним, існують маршрути між будь-якими двома вершинами, а значить, існує і маршрут від вершини k до будь-якої вершини графа. Доведемо, що якщо існує маршрут від вершини k до будь-якої вершини графа i, то граф зв'язний. Дійсно, якщо існує маршрут від k до i, існує також маршрут від i до k. Якщо існує маршрут від k до j, існує також маршрут від j до k. Маршрут від i до j складаємо з двох частин - спочатку від i до k, потім додаємо маршрут від k до j. Отже, від i до j маршрут існує, а тому граф зв'язний. Постановку задачі перевірки графа запишемо у вигляді функції логічного типу. Граф задається матрицею суміжності. Лог Алг зв'язність(ціл n, ціл таб a[1..n, 1..n]) Арг n,a Для перевірки графа достатньо вибрати довільну вершину і перевірити, чи існує шлях від неї до будь-якої іншої. Діятимемо таким чином. Спочатку виберемо довільну вершину (наприклад, першу). Складемо список вершин, до яких існує маршрут довжиною 1від вибраної (тобто суміжних з вибраною). Для кожної з отриманих вершин створимо список вершин, суміжних з нею. Так ми отримаємо вершини, до яких існує маршрут довжиною 1 або 2. Повторюватимемо цей процес далі. Максимальна довжина маршруту дорівнює n-1 ребер (див. малюнок). Зауважимо, що для зберігання вершин доцільно використовувати множинний тип, тому що порядок вершин не є важливим. Отримаємо такий алгоритм Лог Алг зв'язність1(ціл n, ціл таб a[1..n, 1..n]) Арг n,a Поч Множ s Ціл i {довжина шляху}, j, k s:=[1] {початкова вершина} Для i від 2 до n пц Для всіх елементів j, що належать s Отримати всі вершини k такі, що j та k суміжні Додати k до s кц Знач:=s=[1..n] Кін Завдання. Деталізуйте цей алгоритм, перекладіть його мовою Паскаль і перевірте в on-line.
Цей алгоритм не є досконалим. Розглянемо такий граф:
Виконаємо алгоритм "зв'язність1" для цього графа. Коли починається виконання циклу по і, у списку відвіданих вершин міститиметься єдина вершина - перша. Отже, при i>2 для даного прикладу шукати вершини, до яких існує шлях від першої, немає сенсу - вже зрозуміло, що граф зв'язний. Модифікуємо алгоритм зв'язність1 таким чином. Якщо при черговій перевірці до множини додано вершини, необхідно продовжити роботу, а якщо жодної вершини додано не було, очевидно, і не буде додано, і алгоритм повинен завершити свою роботу. Лог Алг зв'язність2(ціл n, ціл таб a[1..n, 1..n]) Арг n,a Поч Множ s Ціл j, k Лог f s:=[1] {початкова вершина} f:=Так Поки f пц f:=Ні Для всіх елементів j, що належать s Отримати всі вершини k такі, що j та k суміжні Якщо k не належить s то f:=Так Додати k до s все кц Знач:=s=[1..n] Кін
Алгоритм зв'язність2 можна покращити, якщо на кожному кроці шукати нову вершину не серед усіх, а тільки серед тих, які ще не відвідувались. Також доцільно шукати вершину, суміжну з новою, не серед усіх відвіданих раніше, а тільки з тих, що було додано на останньому кроці. Пропонується модифікувати алгоритм зв'язність2 самостійно. Розглянемо дещо інший підхід до перевірки графа. Нехай деяка вершина графа a є початковою. Якщо для всіх вершин ця вершина досяжна, граф зв'язний. Нехай b - вершина графа, досяжна з вершини a.
Отже, якщо дві різні вершини a і b досяжні одна з одної, виконується хоча б одна з двох умов: 1) ці вершини суміжні; 2) існує така вершина c, що a і c досяжні одна з одної, а c і b суміжні. Наприклад, якщо вершини графа - аеропорти, а ребра - авіарейси, то звязність такого графа означає можливість дістатись запропонованими рейсами від будь-якого аеропорту до будь-якого іншого. Суміжність вершин - це не що інше як існування прямого рейсу між аеропортами. Нехай ми знаходимось у аеропорту Бориспіль і хочемо потрапити у Хітроу. Отже, Бориспіль - це вершина графа a, а Хітроу - це вершина b. Якщо прямий рейс існує, Бориспіль і Хітроу є суміжними, а значить, і досяжними. Отже, якщо з Борисполя до Хітроу прямого рейсу немає, але з пересадками долетіти можна (наприклад, існують рейси Бориспіль-Франкфурт, Франкфурт-Мадрид і Мадрид-Хітроу), то вершини графа будуть досяжними, але не суміжними. В такому випадку перша умова не виконується, а друга виконується. Нехай а - початкова вершина. Назвемо вершину графа, в якій ми знаходимось, поточною. Нехай це вершина b. Додамо її до списку відвіданих. Спробуємо знайти вершини, які ще не відвідувались і які суміжні з поточною. Для кожної такої вершини c відомо, що a і b досяжні (інакше вершина b не стала б поточною), b і c суміжні, тому a і c досяжні. Переходимо до вершини c і виконуємо аналогічні дії для неї. Запишемо описаний вище процес алгоритмічною мовою: Алг Обхід (Ціл k) Поч Додати k до списка відвіданих вершин Для всіх вершин i пц Якщо вершина і не відвідана та вершини i та k суміжні то Обхід(i) все кц Кін Як бачимо, отримано рекурсивний допоміжний алгоритм Обхід. Деталізуємо цей допоміжний алгоритм і побудуємо головний. Лог Алг зв'язність3(ціл n, ціл таб a[1..n, 1..n]) Арг n,a Поч Множ s s:=[] Обхід(1) Знач:=s=[1..n] Кін
Алг Обхід (Ціл k) Поч Ціл i s:=s+[k] Для i від 1 до n пц Якщо і не належить s та a[i,k]>0 то Обхід(i) все кц Кін Означення. Нехай V - множина вершин деякого графа. Підмножина U є компонентою зв'язності графа, якщо кожна пара вершин з множини U є досяжною з будь-якої вершини і не є досяжною з будь-якої іншої. Приклад Граф, зображений на малюнку 2, має 2 компоненти зв'язності - [1..5] та [6..9].
Підрахуємо для заданого графа кількість компонент зв'язності. Граф задаватимемо матрицею суміжності. Алг Компоненти( Ціл n, Ціл Таб a[1..n,1..n], Ціл s) Арг n,a Рез s Поч Множ m Ціл i m:=[] s:=0 Для i від 1 до n пц Якщо i не належить m то s:=s+1 Обхід(i) все кц Кін |