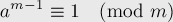Определение
Функция Эйлера 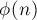 (иногда обозначаемая
(иногда обозначаемая 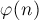 или
или 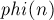 ) — это количество чисел от
) — это количество чисел от  до
до  , взаимно простых с
, взаимно простых с  . Иными словами, это количество таких чисел в отрезке
. Иными словами, это количество таких чисел в отрезке ![[1; n]](https://e-maxx.ru/tex2png/cache/69cc1de918936aa552092962896df9f8.png) , наибольший общий делитель которых с
, наибольший общий делитель которых с  равен единице.
равен единице.
Несколько первых значений этой функции (A000010 в энциклопедии OEIS):
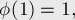
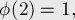
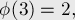
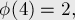
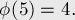
Свойства
Три следующих простых свойства функции Эйлера — достаточны, чтобы научиться вычислять её для любых чисел:
- Если
 — простое число, то
— простое число, то 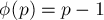 .
.
(Это очевидно, т.к. любое число, кроме самого
 , взаимно просто с ним.)
, взаимно просто с ним.) - Если
 — простое,
— простое,  — натуральное число, то
— натуральное число, то 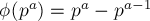 .
.
(Поскольку с числом
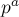 не взаимно просты только числа вида
не взаимно просты только числа вида 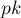
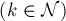 , которых
, которых 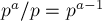 штук.)
штук.) - Если
 и
и  взаимно простые, то
взаимно простые, то 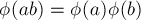 ("мультипликативность" функции Эйлера).
("мультипликативность" функции Эйлера).
(Этот факт следует из китайской теоремы об остатках. Рассмотрим произвольное число
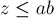 . Обозначим через
. Обозначим через  и
и  остатки от деления
остатки от деления 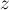 на
на  и
и  соответственно. Тогда
соответственно. Тогда 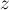 взаимно просто с
взаимно просто с 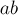 тогда и только тогда, когда
тогда и только тогда, когда 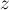 взаимно просто с
взаимно просто с  и с
и с  по отдельности, или, что то же самое,
по отдельности, или, что то же самое,  взаимно просто с
взаимно просто с  и
и  взаимно просто с
взаимно просто с  . Применяя китайскую теорему об остатках, получаем, что любой паре чисел
. Применяя китайскую теорему об остатках, получаем, что любой паре чисел  и
и 
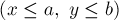 взаимно однозначно соответствует число
взаимно однозначно соответствует число 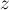
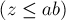 , что и завершает доказательство.)
, что и завершает доказательство.)
Отсюда можно получить функцию Эйлера для любого 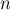 через его факторизацию (разложение
через его факторизацию (разложение  на простые сомножители):
на простые сомножители):
если
![n = p_1^{a_1} \cdot p_2^{a_2} \cdot \ldots \cdot [...]](https://e-maxx.ru/tex2png/cache/3d3e83493513e2058c3835f438a7a37b.png)
(где все 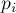 — простые), то
— простые), то
![\phi(n) = \phi(p_1^{a_1}) \cdot \phi(p_2^{a_2}) \[...]](https://e-maxx.ru/tex2png/cache/146722a63b75ce3841aae9cb02f06cac.png)
![= (p_1^{a_1} - p_1^{a_1-1}) \cdot (p_2^{a_2} - p_[...]](https://e-maxx.ru/tex2png/cache/589f0d28922891ee426452eba24e3af1.png)
![= n \cdot \left( 1-{1\over p_1} \right) \cdot \le[...]](https://e-maxx.ru/tex2png/cache/3ca03d151f2c44851d626e5a6c9df921.png)
Реализация
Простейший код, вычисляющий функцию Эйлера, факторизуя число элементарным методом за 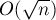 :
:
int phi (int n) {
int result = n;
for (int i=2; i*i<=n; ++i)
if (n % i == 0) {
while (n % i == 0)
n /= i;
result -= result / i;
}
if (n > 1)
result -= result / n;
return result;
}
Ключевое место для вычисление функции Эйлера — это нахождение факторизации числа  . Его можно осуществить за время, значительно меньшее
. Его можно осуществить за время, значительно меньшее 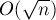 : см. Эффективные алгоритмы факторизации.
: см. Эффективные алгоритмы факторизации.
Приложения функции Эйлера
Самое известное и важное свойство функции Эйлера выражается в теореме Эйлера:
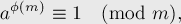
где 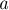 и
и 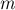 взаимно просты.
взаимно просты.
В частном случае, когда 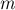 простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
простое, теорема Эйлера превращается в так называемую малую теорему Ферма: